遍历二维矩阵的各种花样
PS:干货很多,建议分多次食用
常规遍历
1 | # 输出以下序列: [1 2 3 4...15 16] |
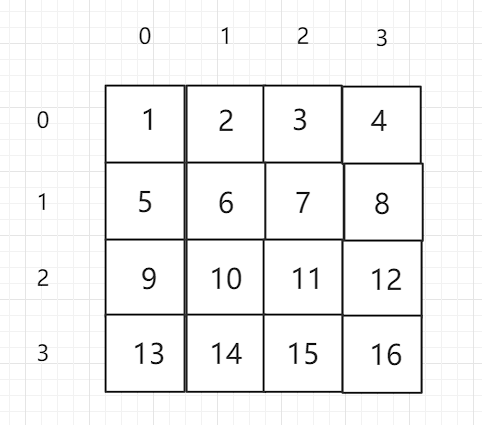
这个就是按行遍历即可
示例代码
1 | int len = matrix.length; |
旋转遍历
PS:本遍历方法使用生成以下矩阵来讲述,生成会了,遍历自然也会了
示意图
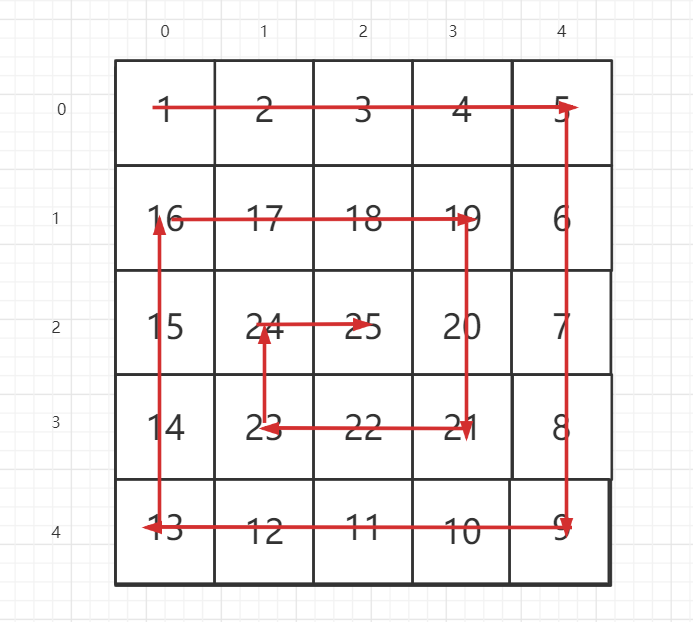
遍历思路
1 | # [0,0] [0,1] [0,2] [0,3] 👉向右 |
圈圈法
第一个思路就是一圈一圈的遍历
将每一个圈拆为四个部分
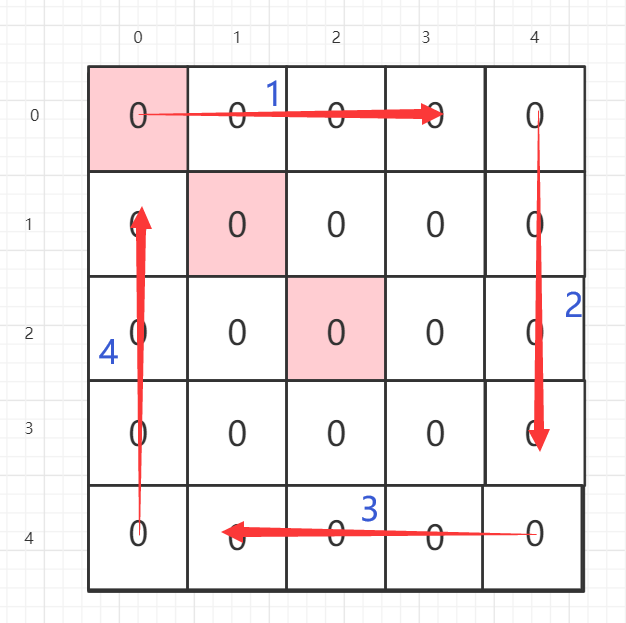
第一个循环用来生成水平向左的数据
第二个循环用来生成垂直向下的数据
第三个循环用来生成水平向右的数据
第四个循环用来生成垂直向上的数据
流程图
粉红色的是标注为每次大循环的开始处
PS:图片很多,过程很详细
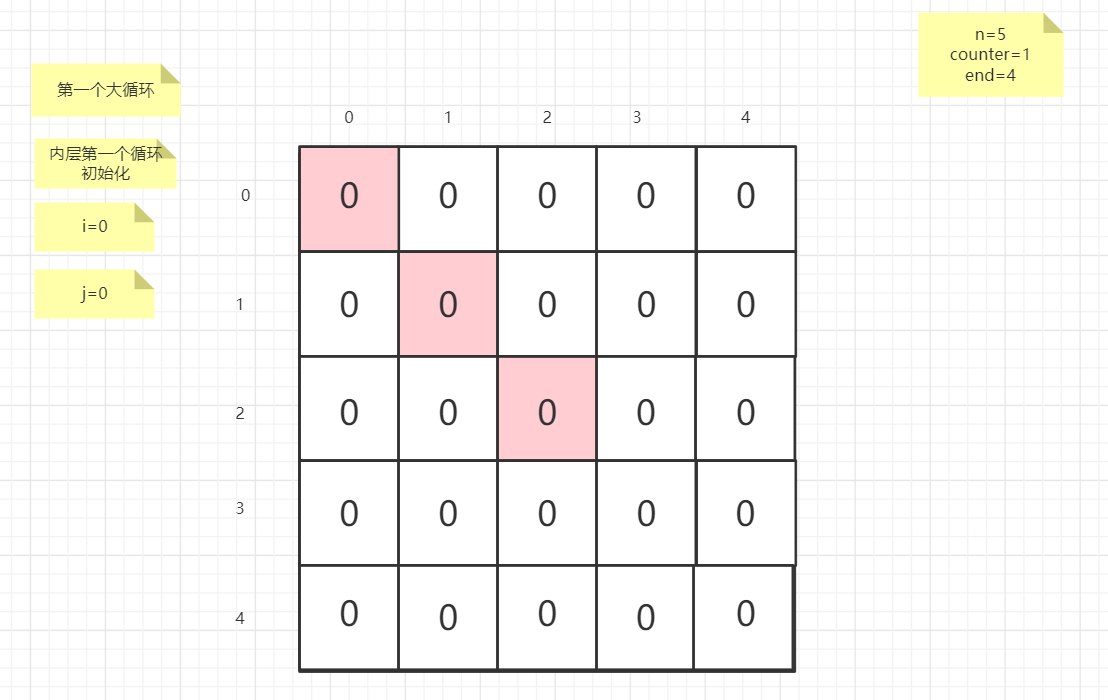
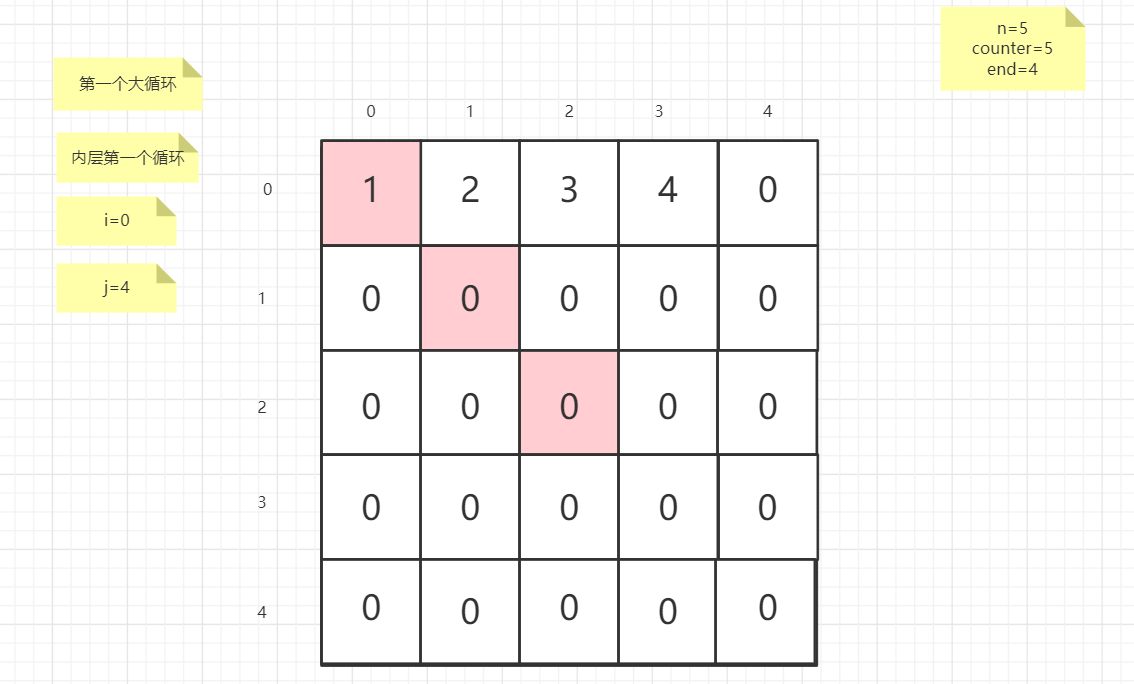
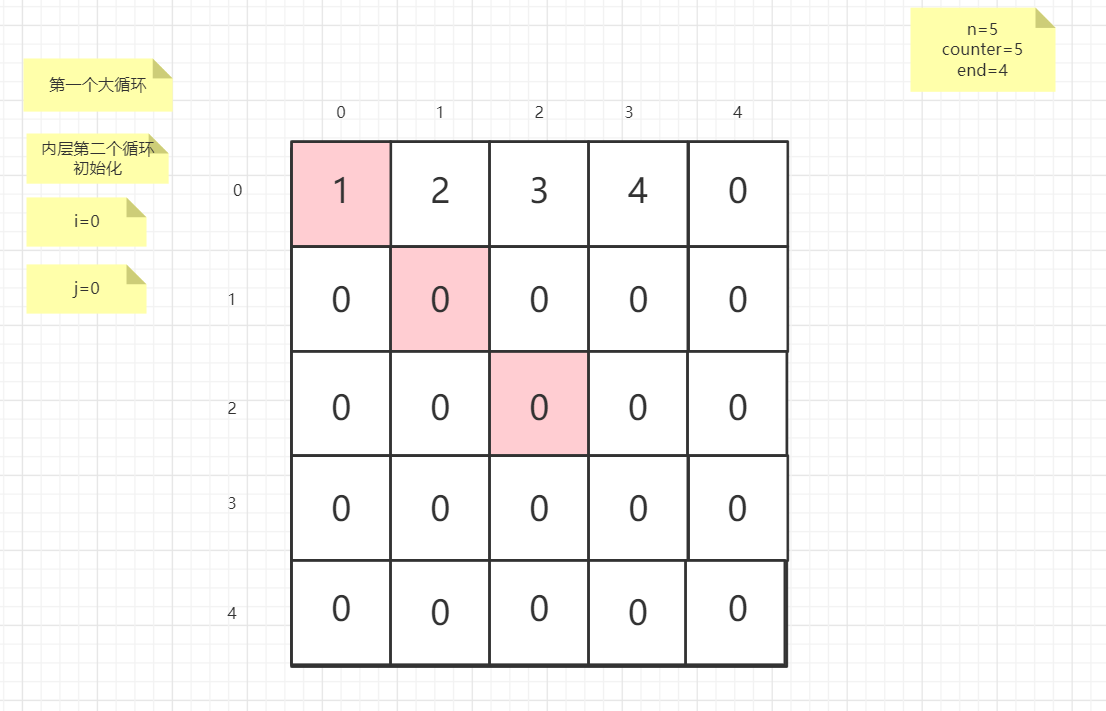
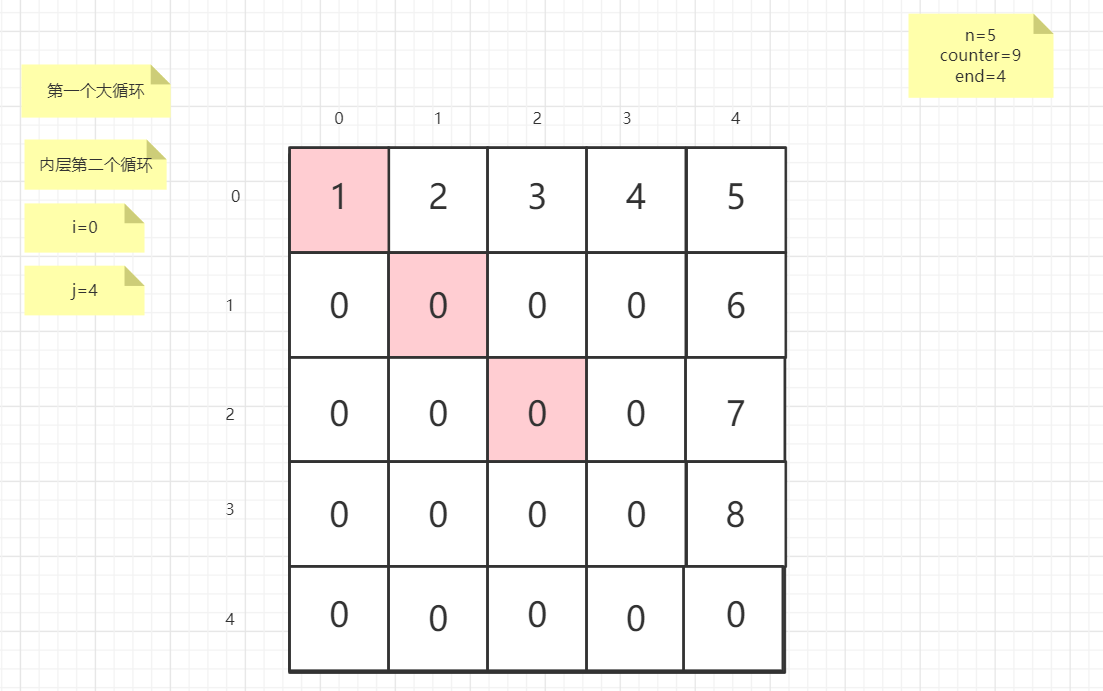
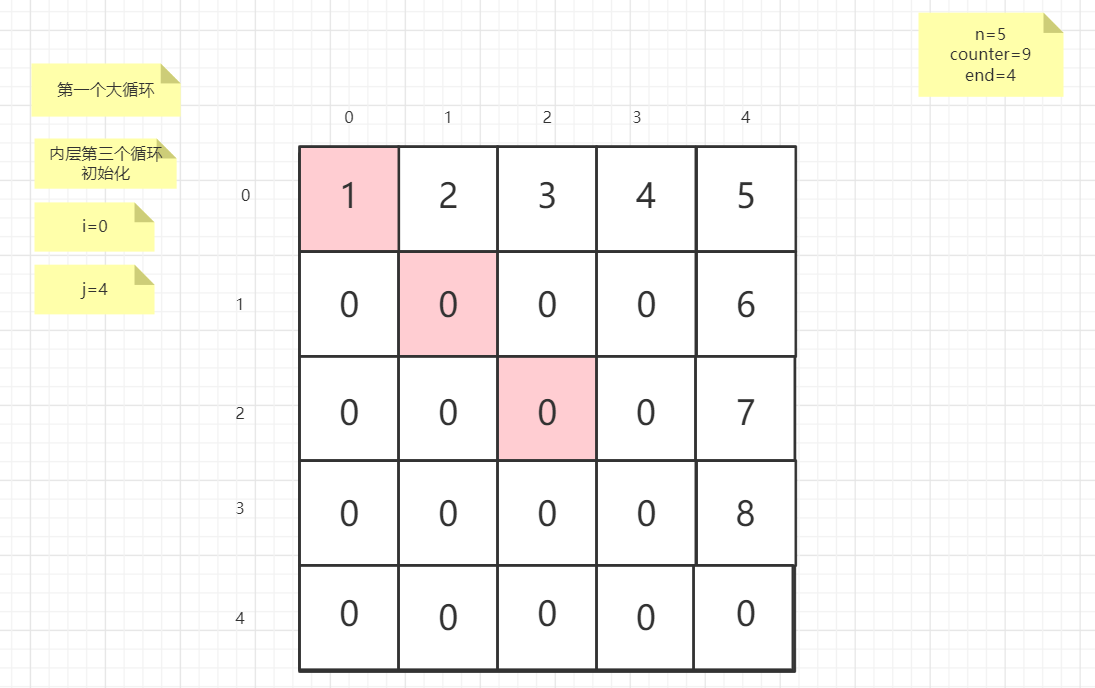
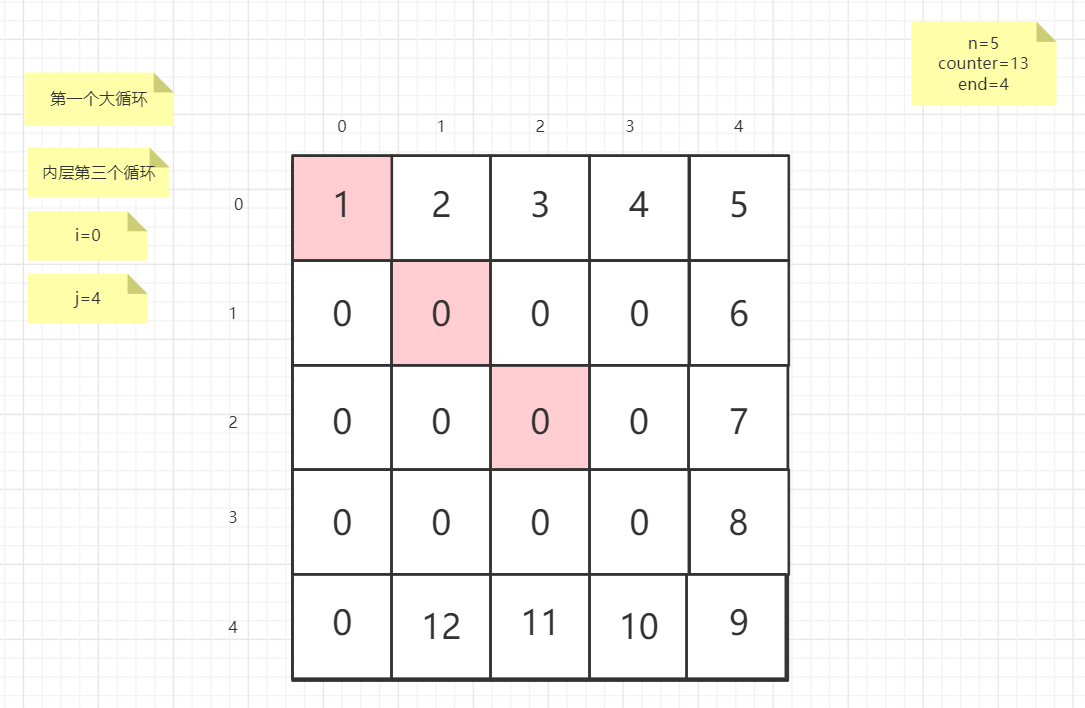
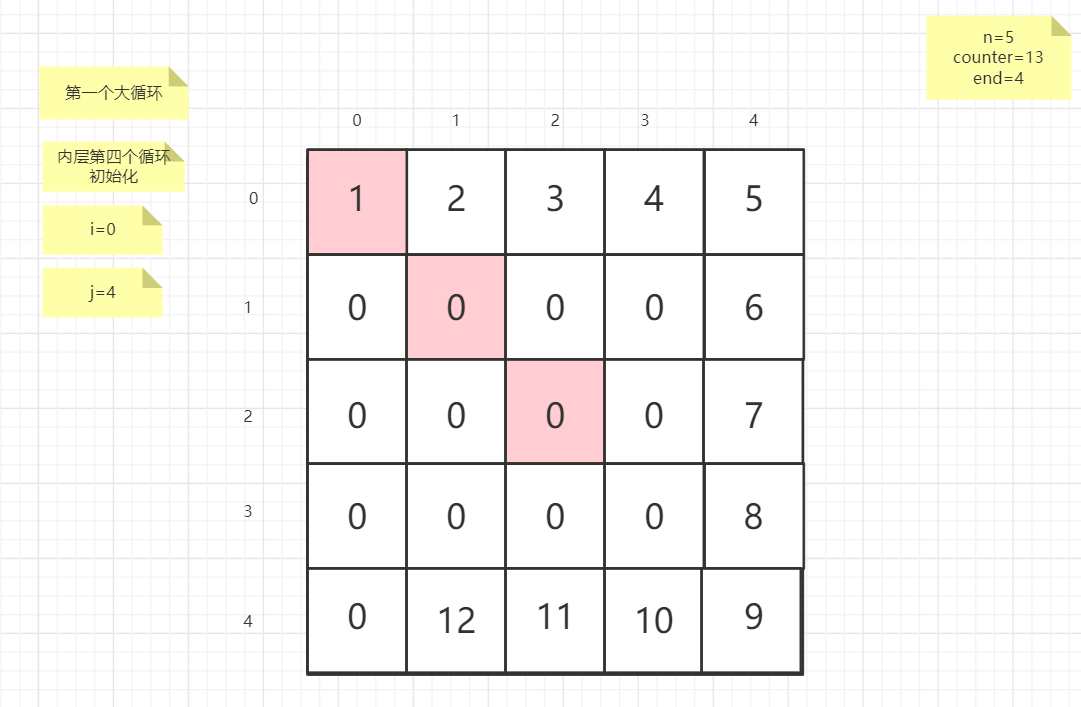
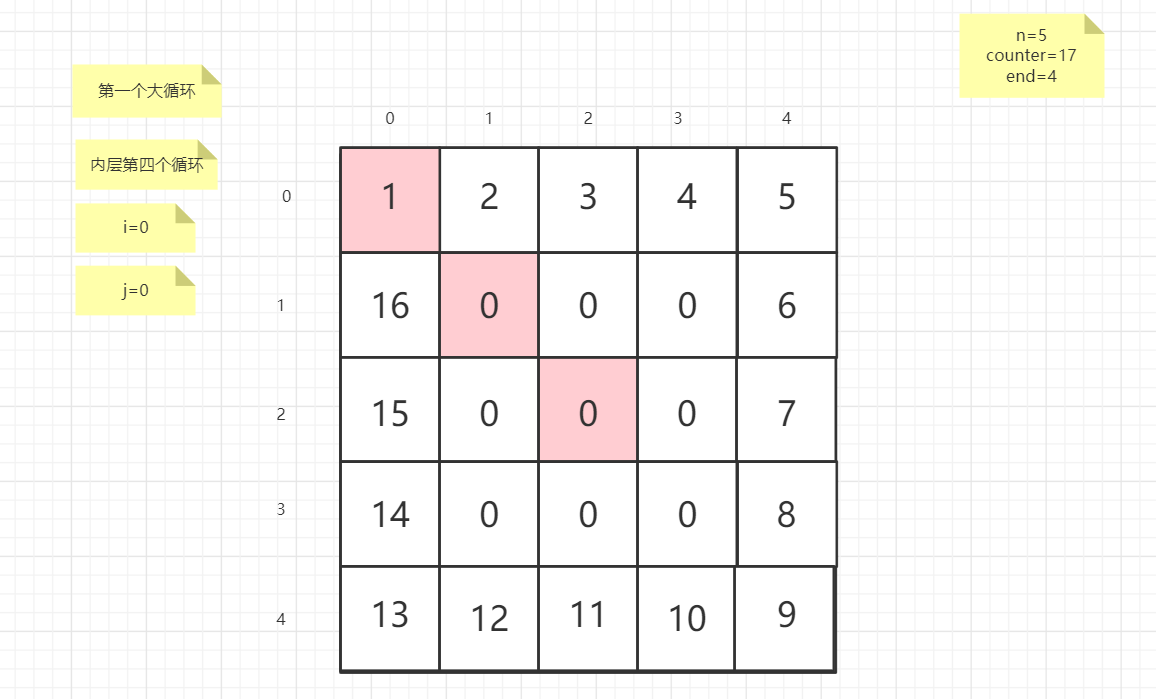
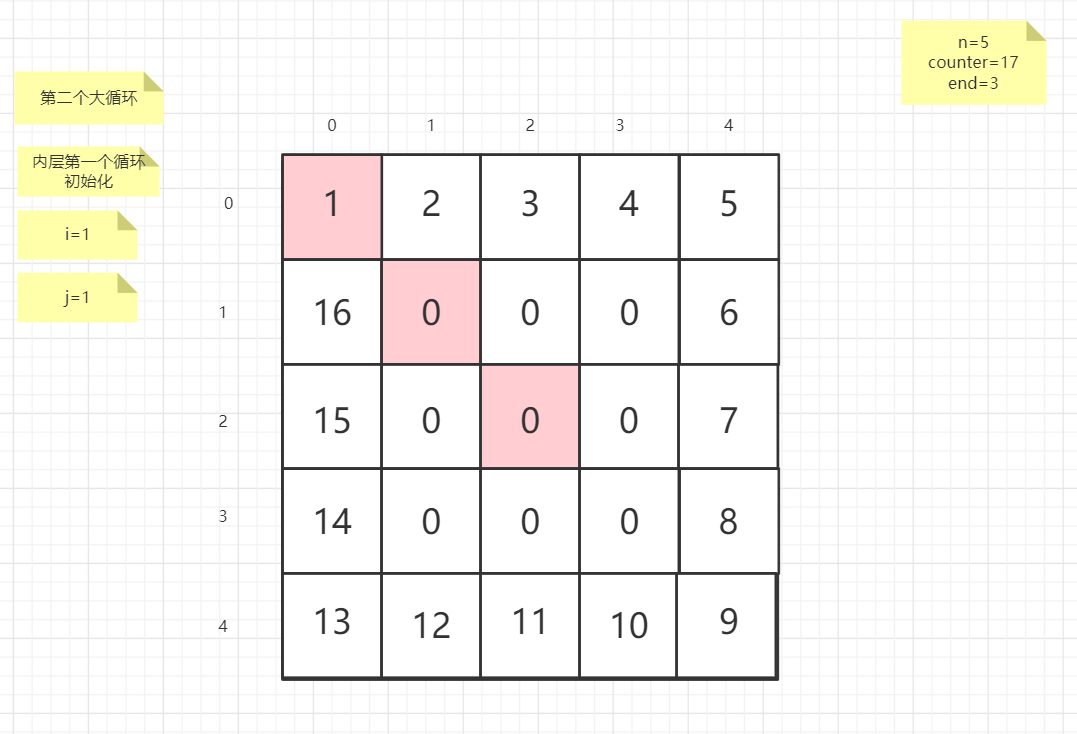
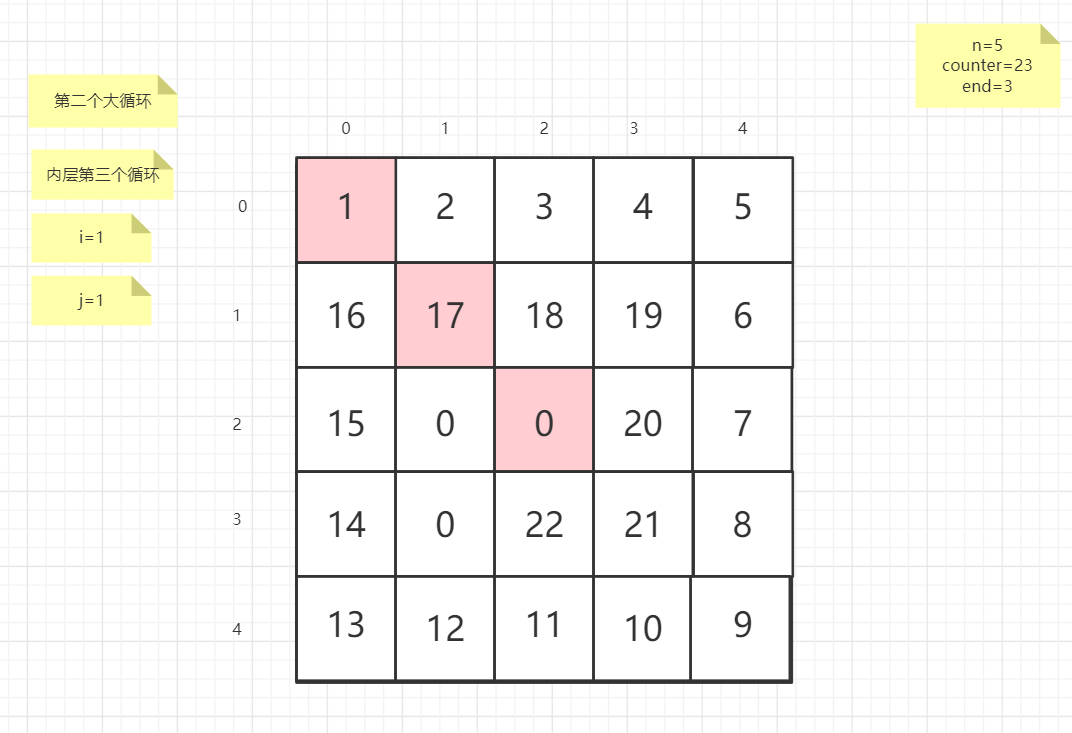
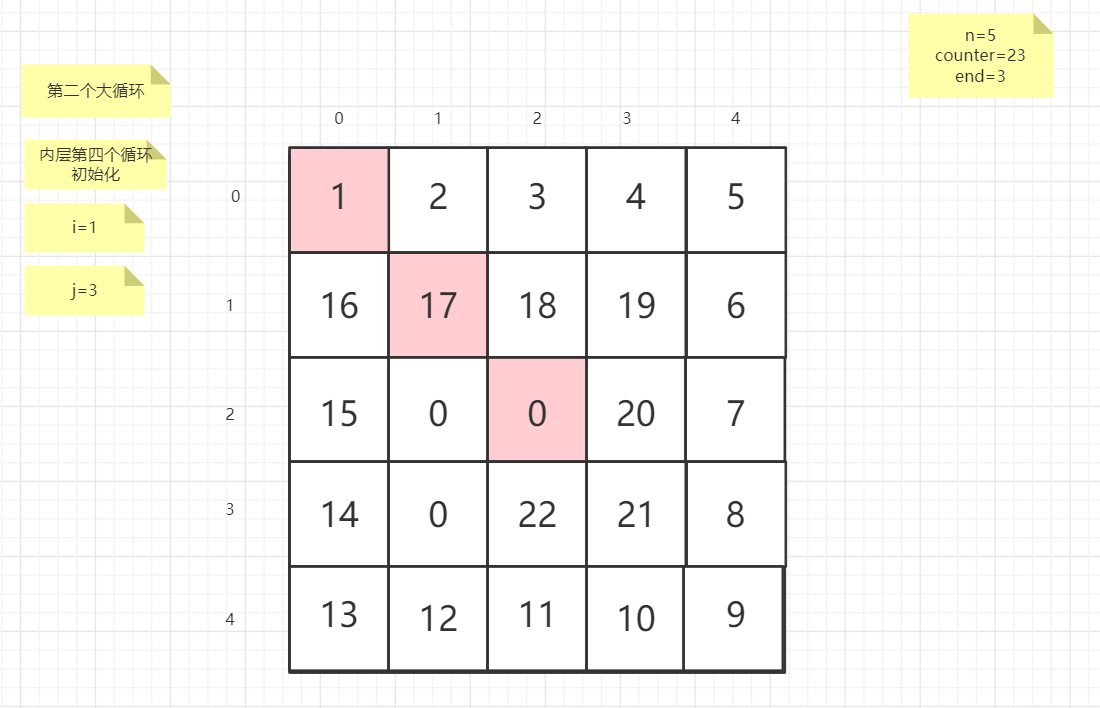
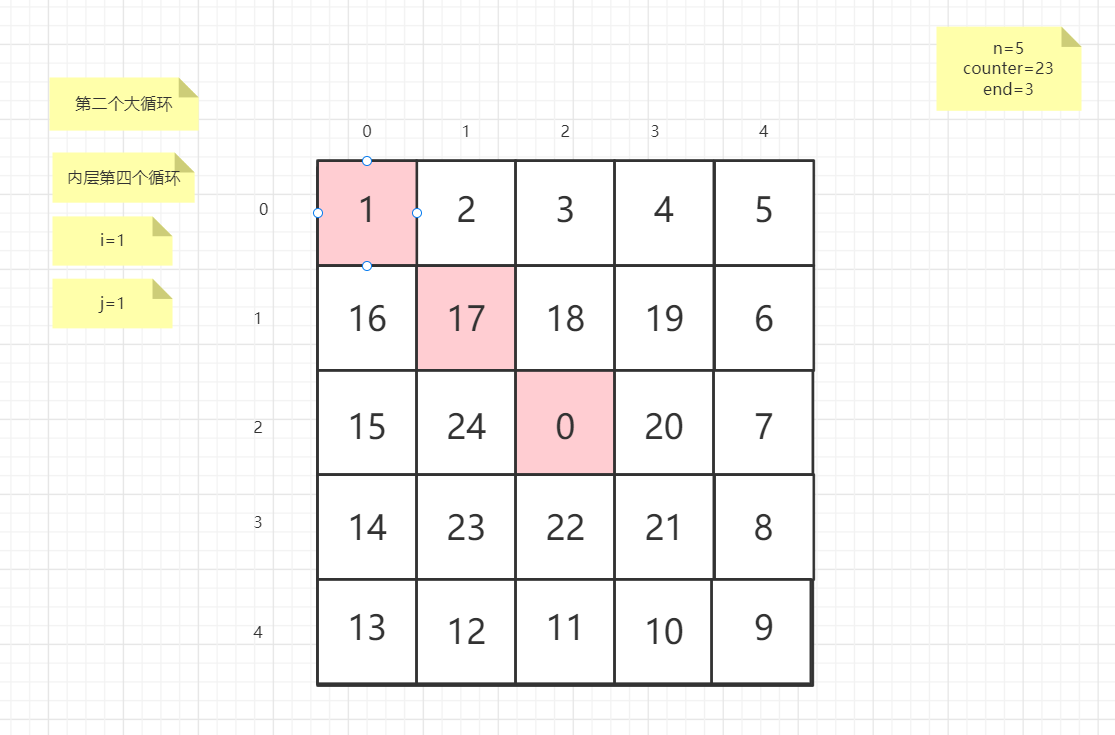
示例代码
1 | public int[][] rotateNumber(int n) { |
横平竖直法(推荐)
这种方法是通过四个边界来辅助生成矩阵
四个边界的示意图
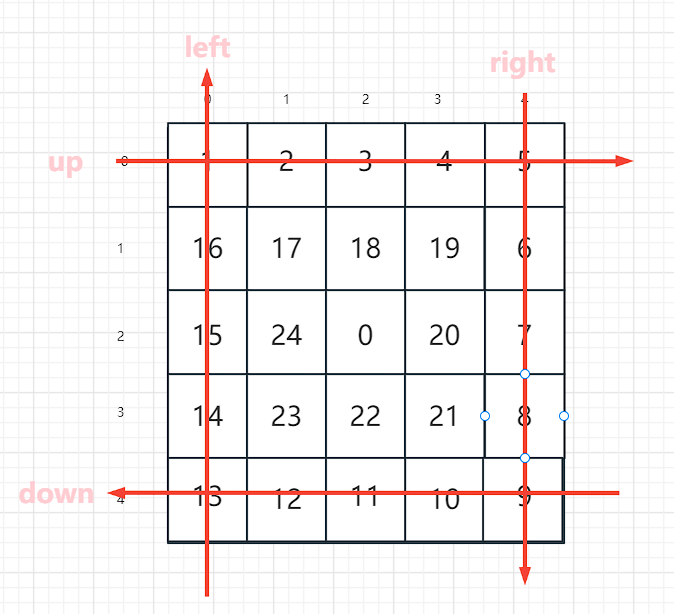
示例代码
1 | public int[][] rotateNumber(int n){ |
斜遍历
1 | # 输出所有由左上向右下方向的对角线: [13 9 14 5 10 15 1 6 11 16 2 7 12 3 8 4] |
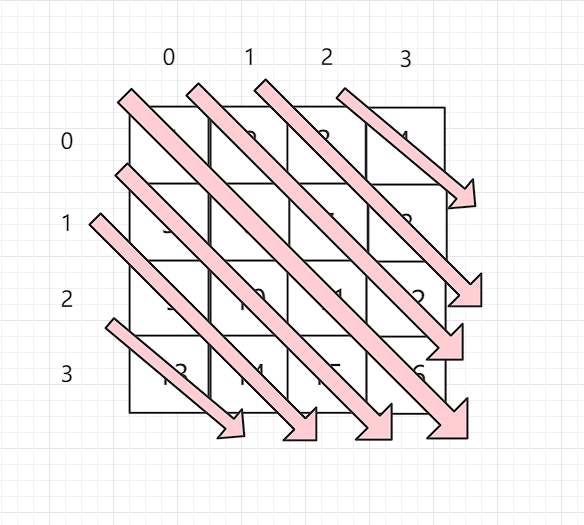
偏移X法
和往常一样遍历第一行,[0,0] [0,1] [0,2] [0,3] [0,4]
可以发现中间那个对角线是这一行向下偏移的结果,但是不同的位置在 X 方向上的偏移量是不一样的
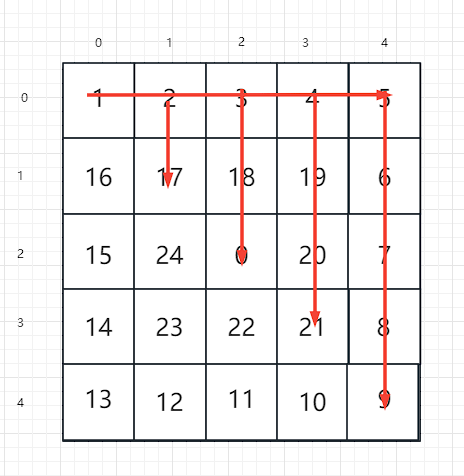
遍历第二行[1,0] [1,1] [1,2] [1,3] [1,4]
可以看到和刚刚第一行一样,每一列向下偏移一定量就可以得到主对角线下面的那个对角线了
(这里先不要管越界的问题,先把思路理清楚,再在代码里面解决越界问题)
先写出遍历每一行的初始代码,然后我们在这个上面改造
1 | for (int i = 0; i < len; i++) { |
在遍历每一行的情况,向下偏移就是对角线了
每一列的偏移量都是不一样的,接下来要解决的就是如何算出每一列的偏移量
经过观察可以发现,当前这一列的偏移量就是当前的列值,那么就好办了直接用j就可以了
1 | for (int i = 0; i < len; i++) { |
现在还有一个问题,就是得到的对角线是部分不合法的,那么接下来就是如何截取合法的对角线部分
因为对角线是由每一行向下偏移而来,对角线越界的根本原因是每一行遍历多了
那么只要逐渐减少每一行的遍历长度即可,每一行少遍历 i 的长度即可
1 | for (int i = 0; i < len; i++) { |
完整示例代码
PS:注意右上角
1 | for (int i = len - 1; i >= 0; i--) { |
偏移Y法
这个方法和偏移 X 法有异曲同工之妙
只不过从遍历每一行变成了遍历每一列
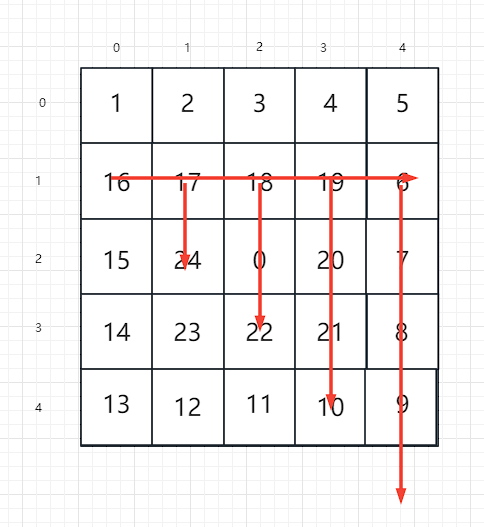
和刚刚一样,先写出遍历每一列
1 | for (int j = 0; j < len; j++) { |
然后向右边偏移
1 | for (int j = 0; j < len; j++) { |
对角线不合法,截取合法部分
1 | for (int j = 0; j < len; j++) { |
完整示例代码
PS:注意左下角
1 | for (int j = 0; j < len; j++) { |
偏移对角线法(推荐)
可以发现偏移 X 法和偏移 Y 法都比较麻烦
所以我比较推荐这种方法,根据对角线来做偏移就会简单很多
从左上顶角到右下顶角的那条对角线如下[0,0] [1,1] [2,2] [3,3]
@表示越界舍弃
整体往下偏移 1 位,就是[1,0] [2,1] [3,2] [4,3](@)
整体往下偏移 2 位,就是[2,0] [3,1] [4,2](@) [5,3](@)
整体往下偏移 3 位,就是[3,0] [4,1] [5,2](@) [6,3](@)
整体往上偏移 1 位,就是[-1,0](@) [0,1] [1,2] [2,3]
整体往上偏移 2 位,就是[-2,0](@) [-1,1](@) [-1,0][0,2] [1,3]
整体往上偏移 3 位,就是[-3,0](@) [-2,1](@) [-1,2](@) [0,3]
如何解决越界
既然完整的对角线偏移会出现越界,那就偏移部分的对角线不就行了
1 | int len = matrix.length; |
在理解了上述的方法后,修改下来完成第一部分的遍历,即这一块的遍历
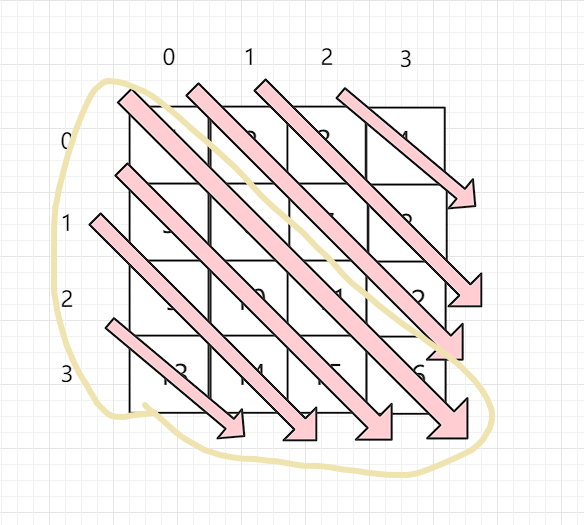
这个和刚刚不同的地方在于它的偏移量是从大到小的,上面那个理解了,这个应该也不难
1 | // [3,0] |
完整示例代码
1 | public void tiltPrint(int[][] matrix){ |
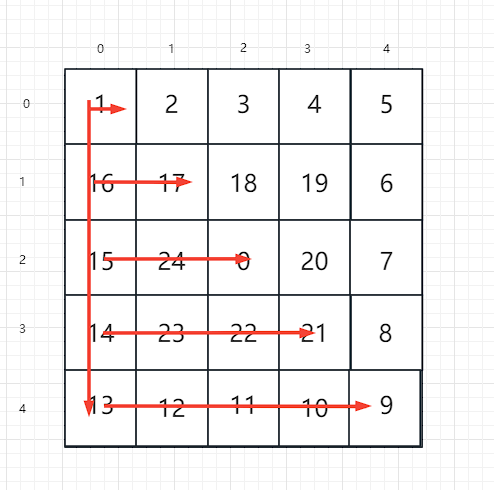
螺旋遍历
1 | # 输出螺旋遍历顺序: [1 2 3 4 5 6 7 8 9 10 11 ... 21] |
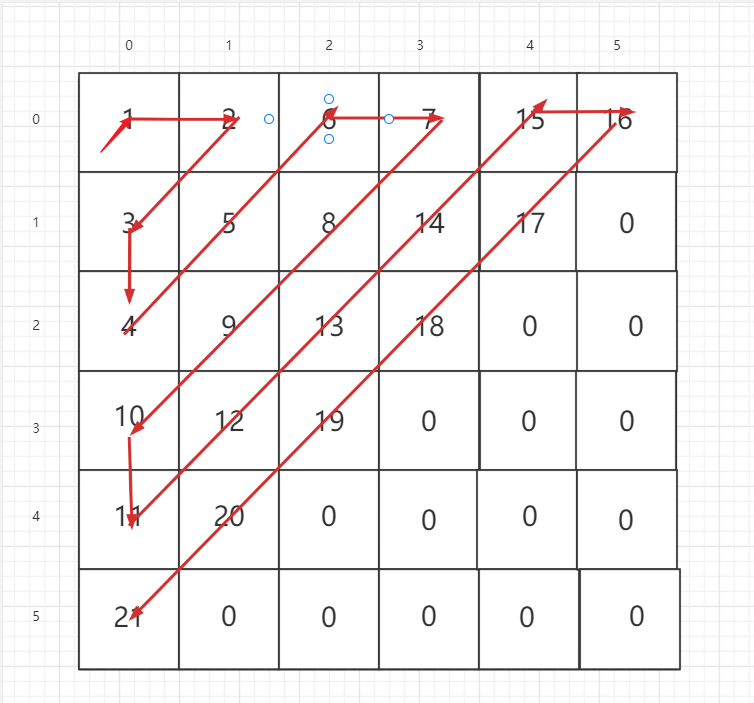
拆解法
将这个路径拆解开
拆解如下
1 | # [0,0] -- [0,1] [1,0] |
流程图
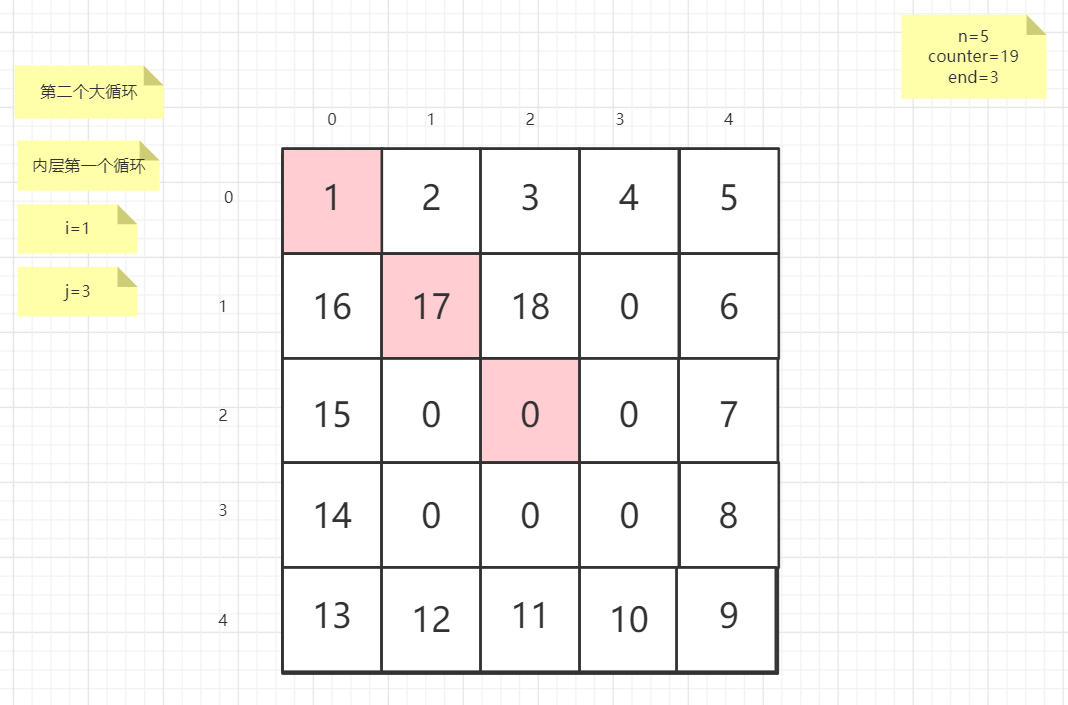
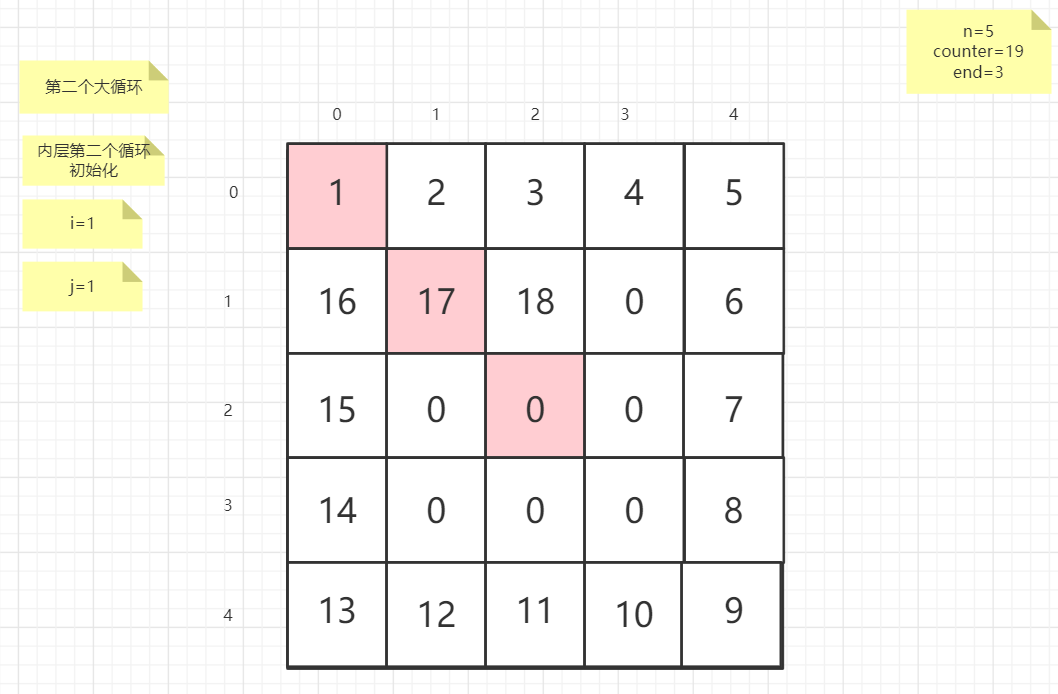
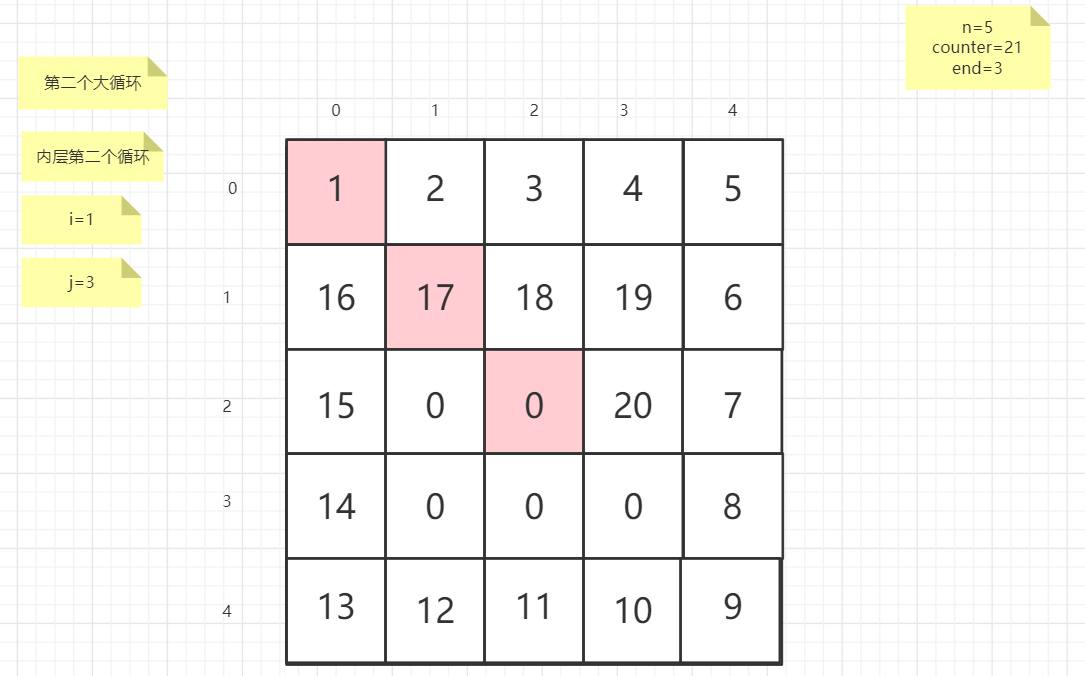
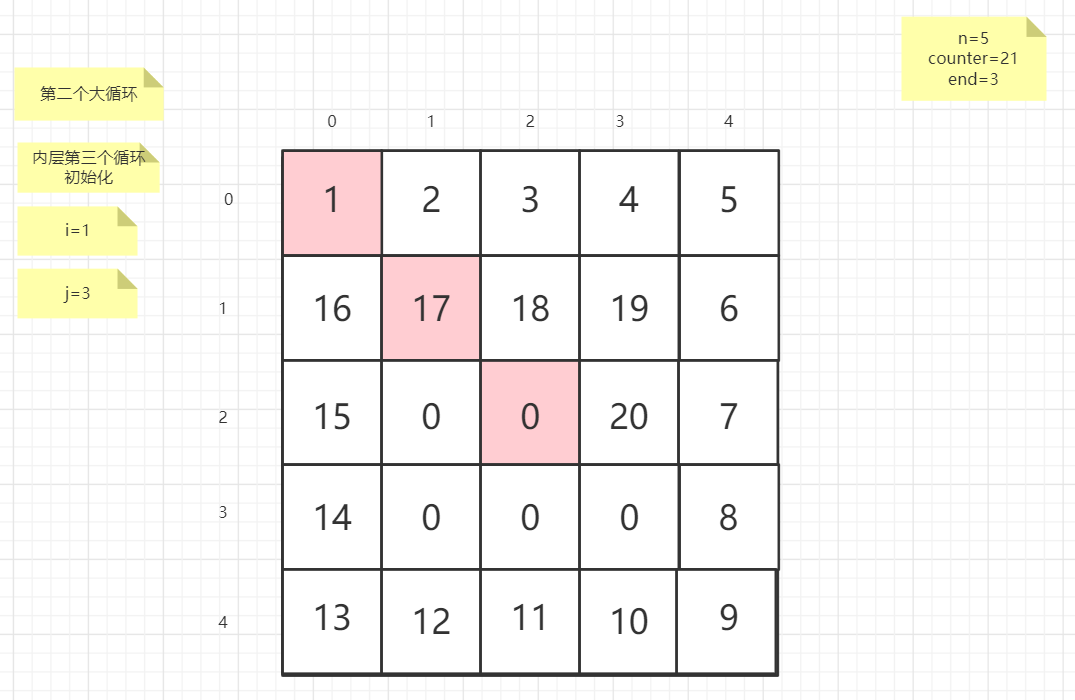
粉红色的是标注为每次大循环的开始处
标注内层循环初始化的是该循环刚要开始时候的数据
PS:图片很多,过程很详细
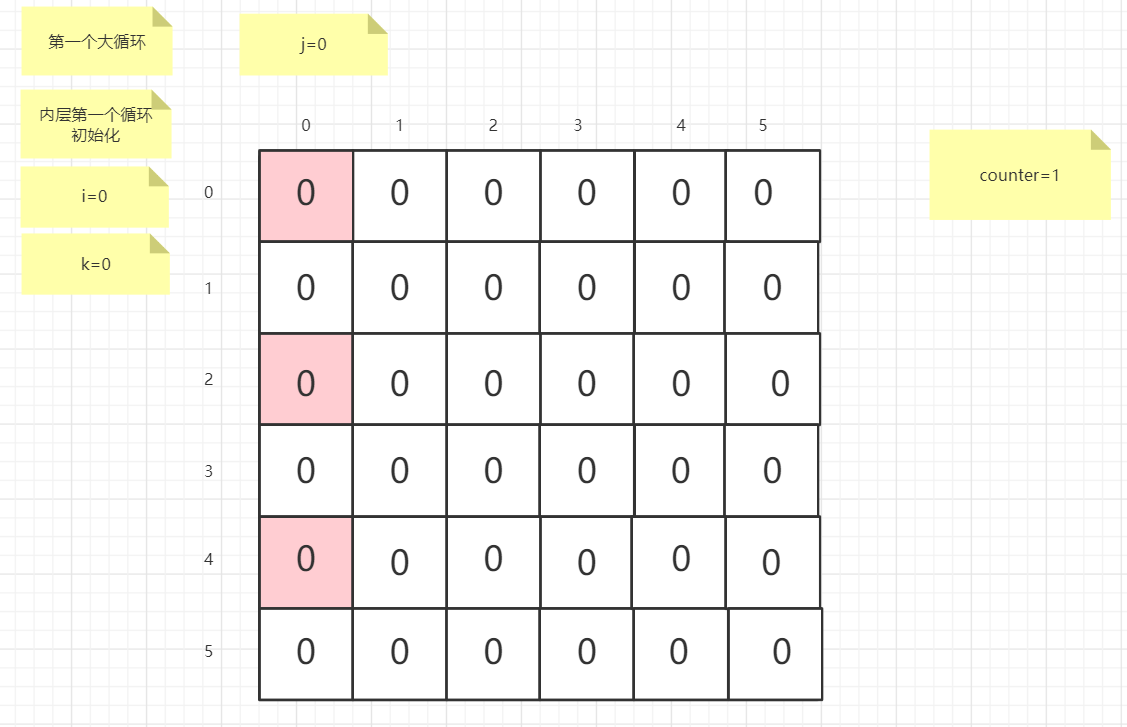
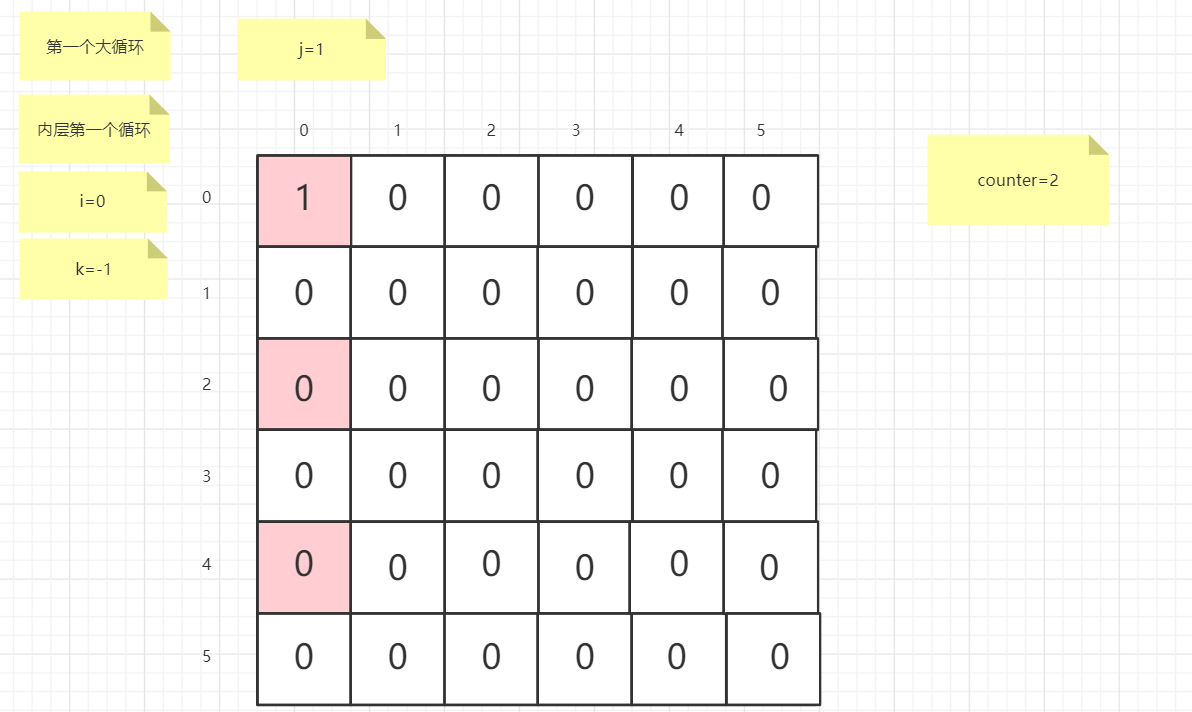
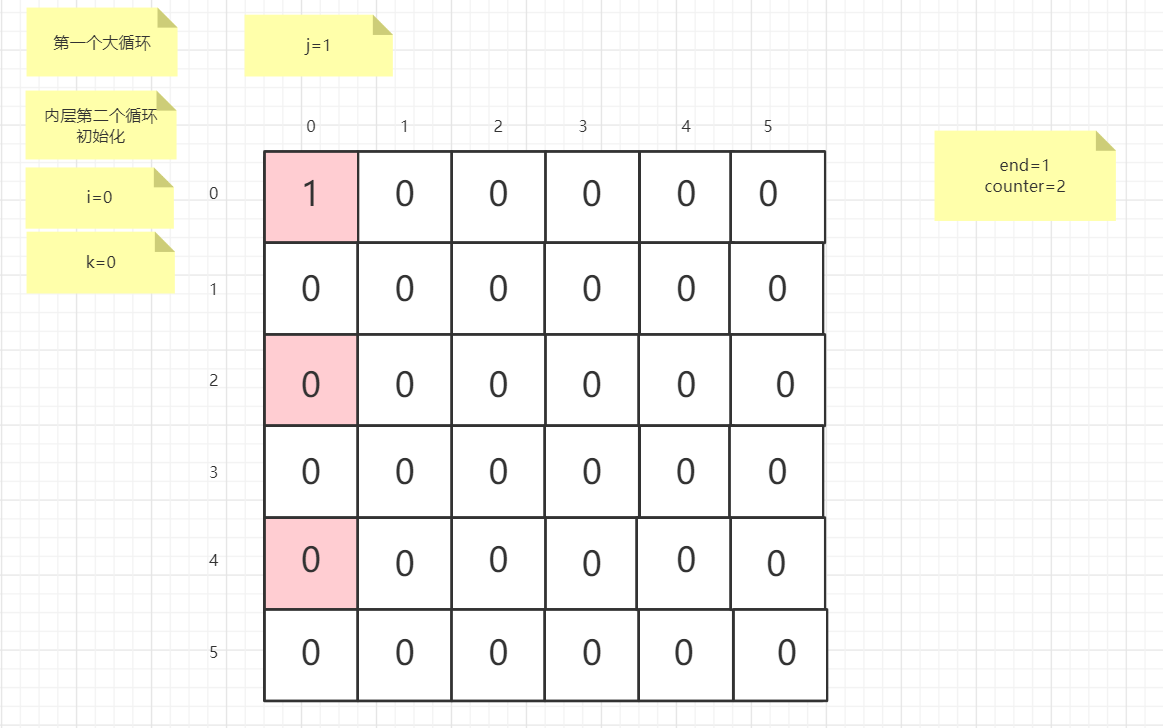
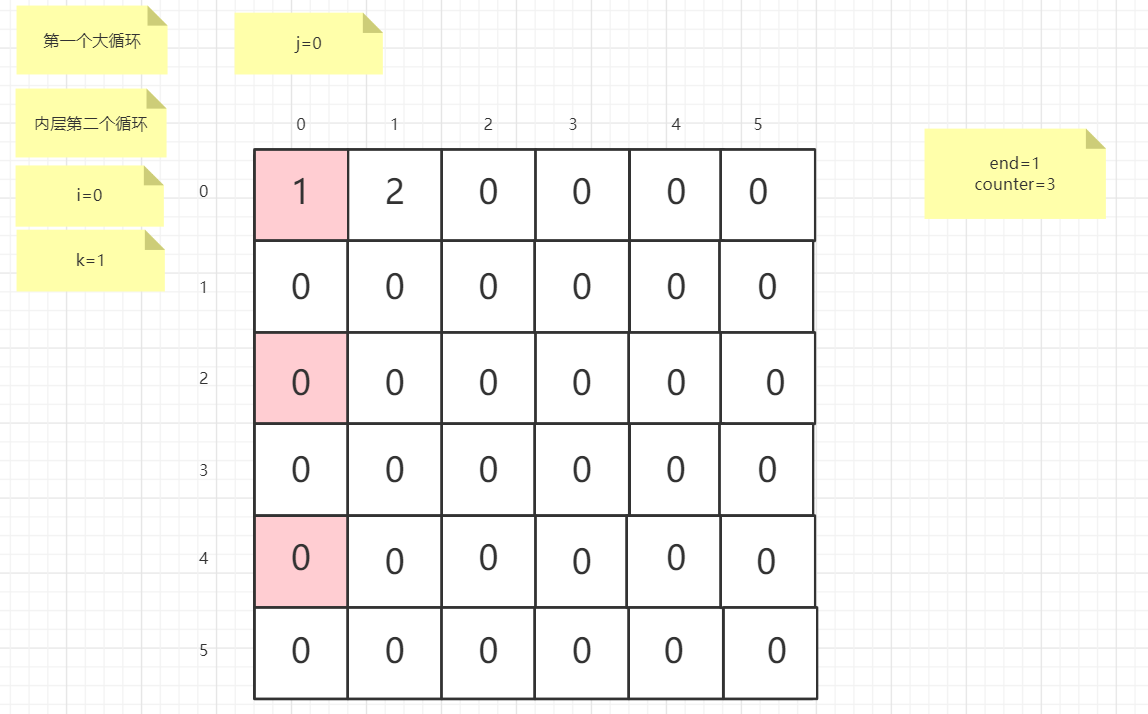
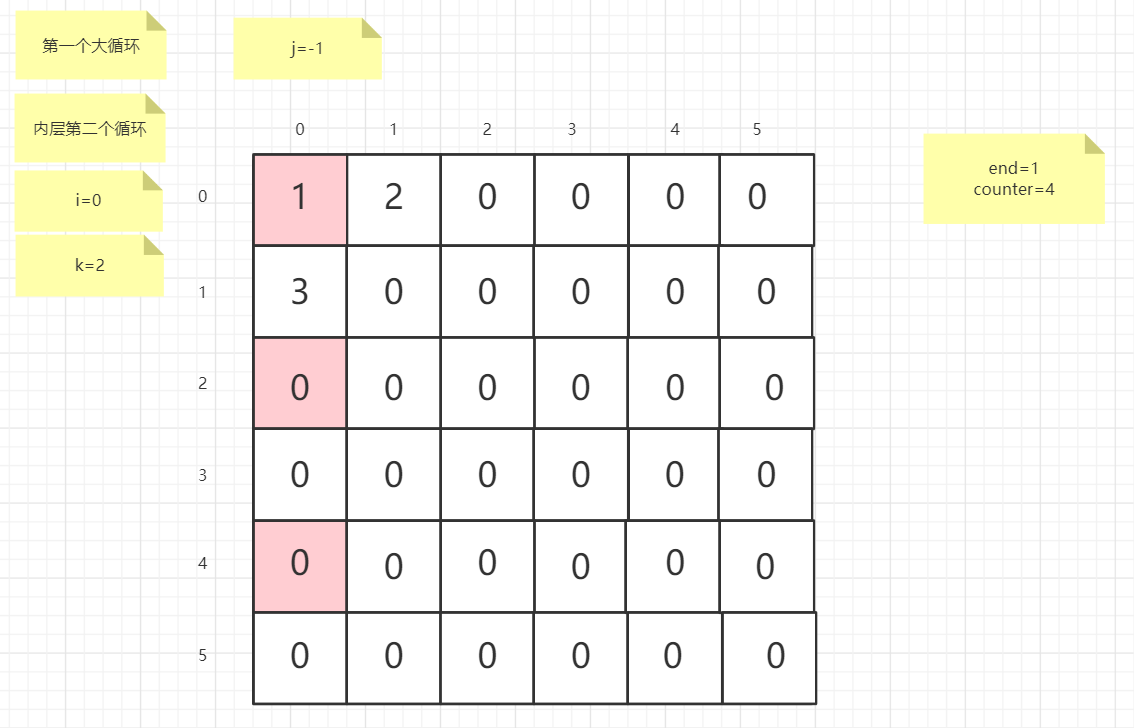
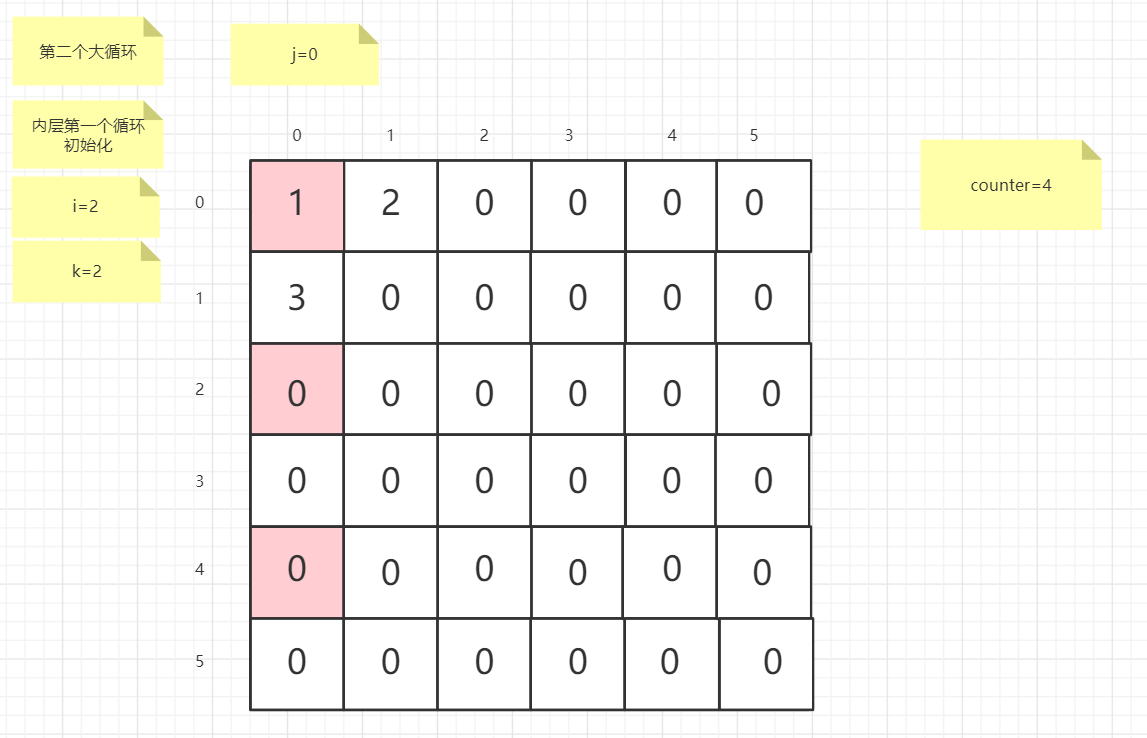
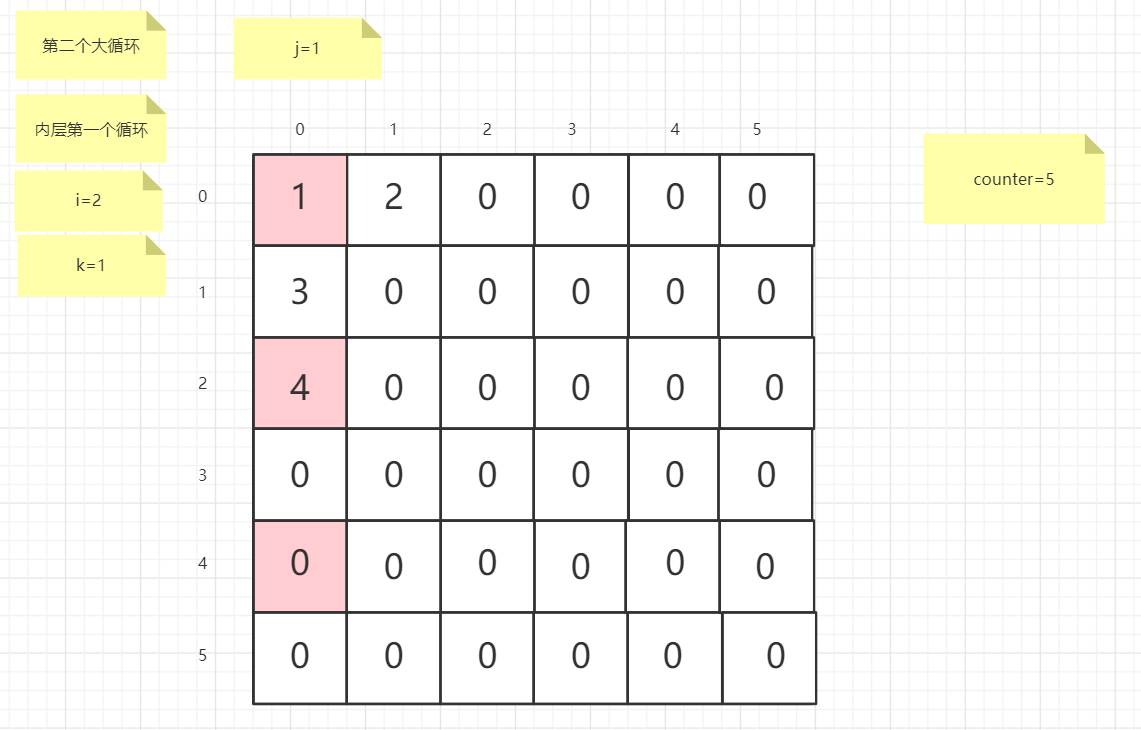
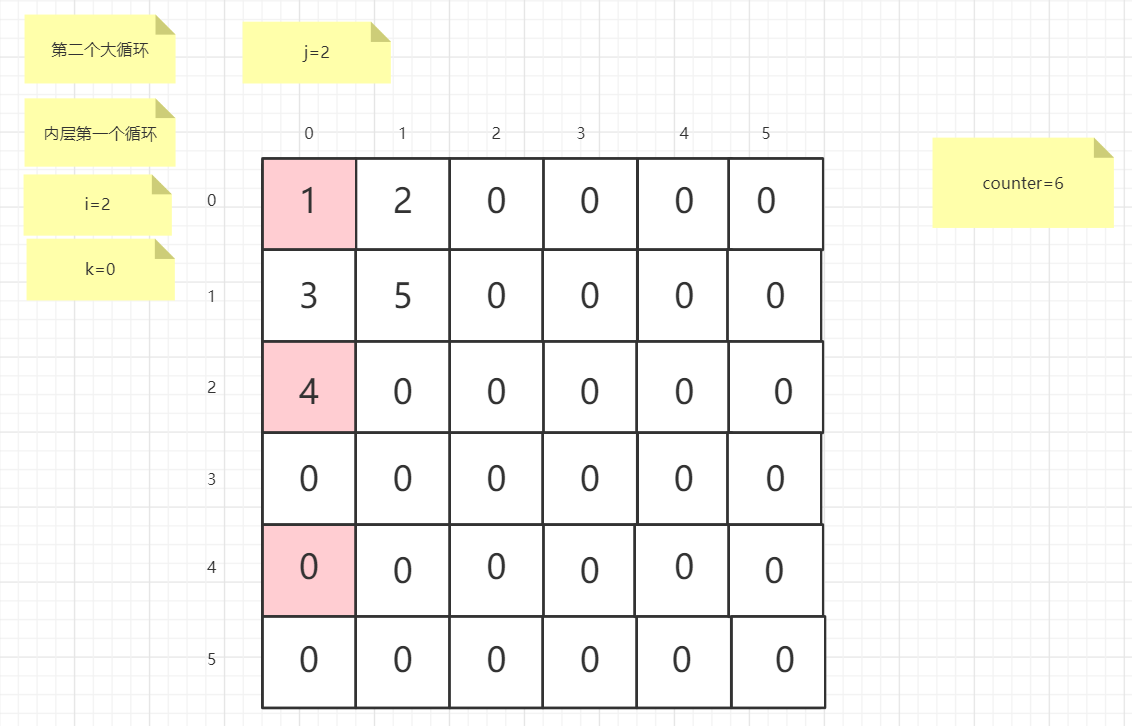
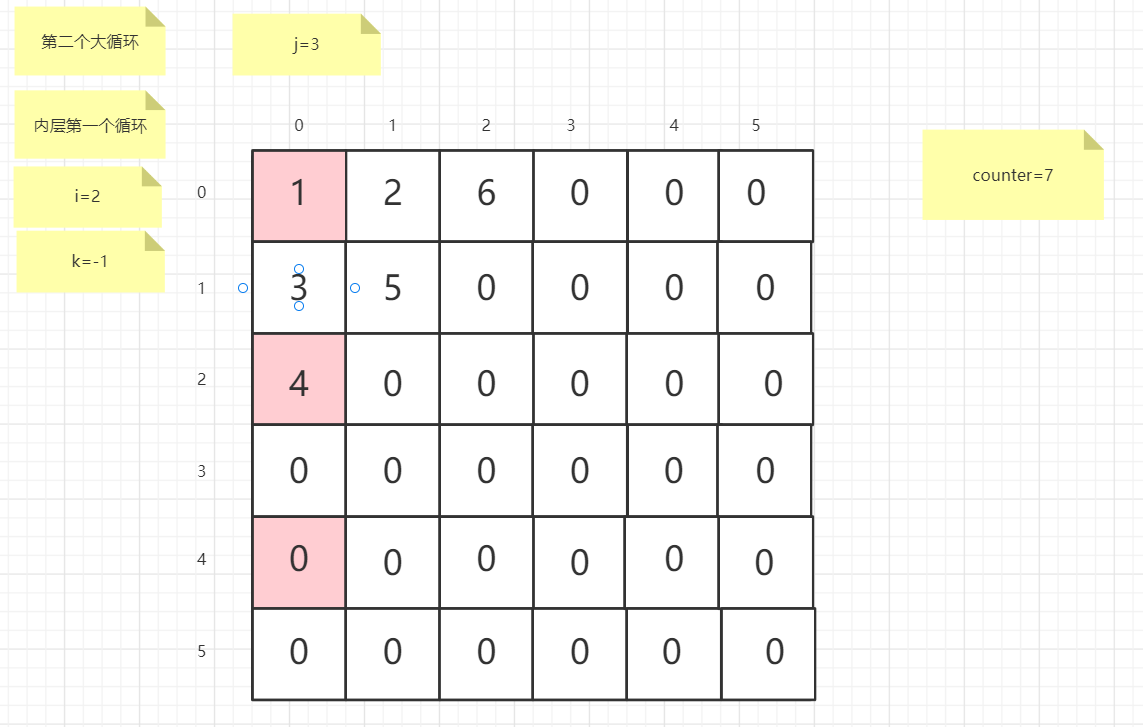
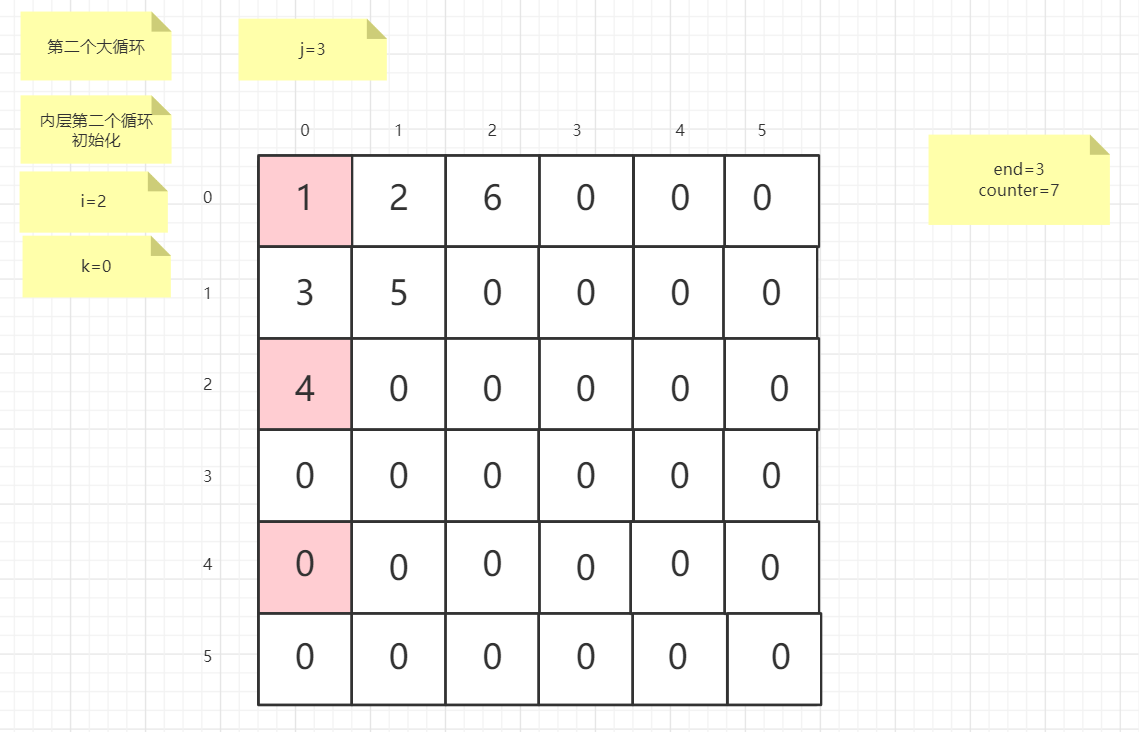
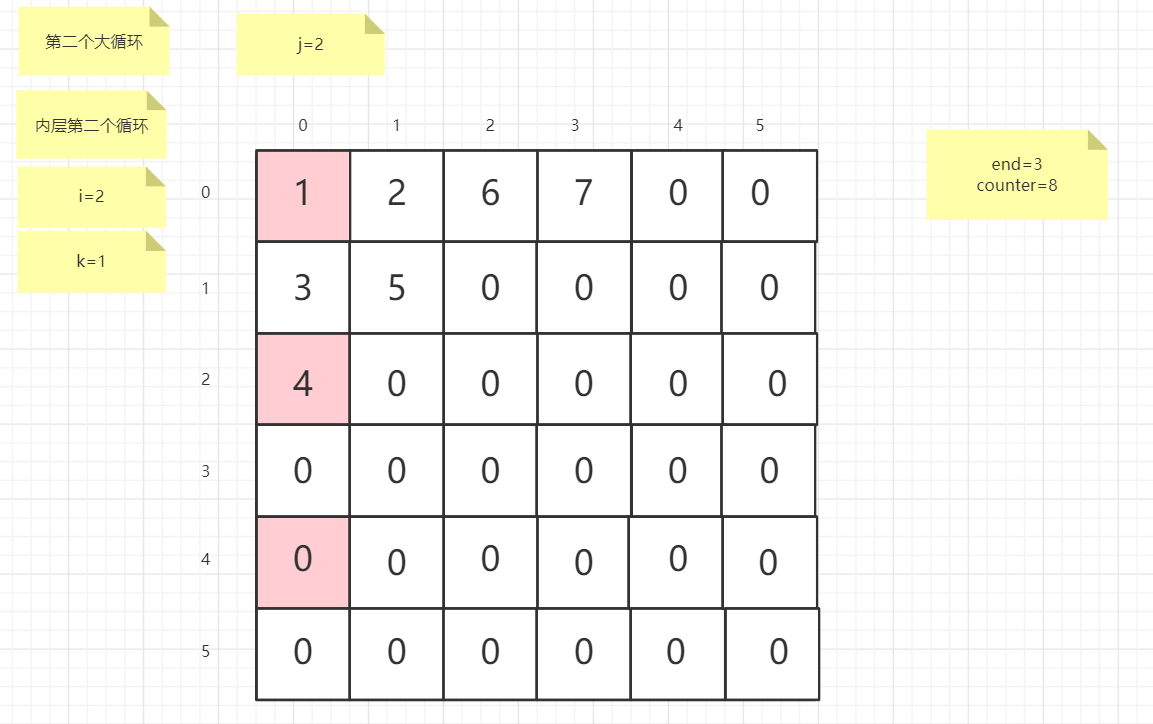
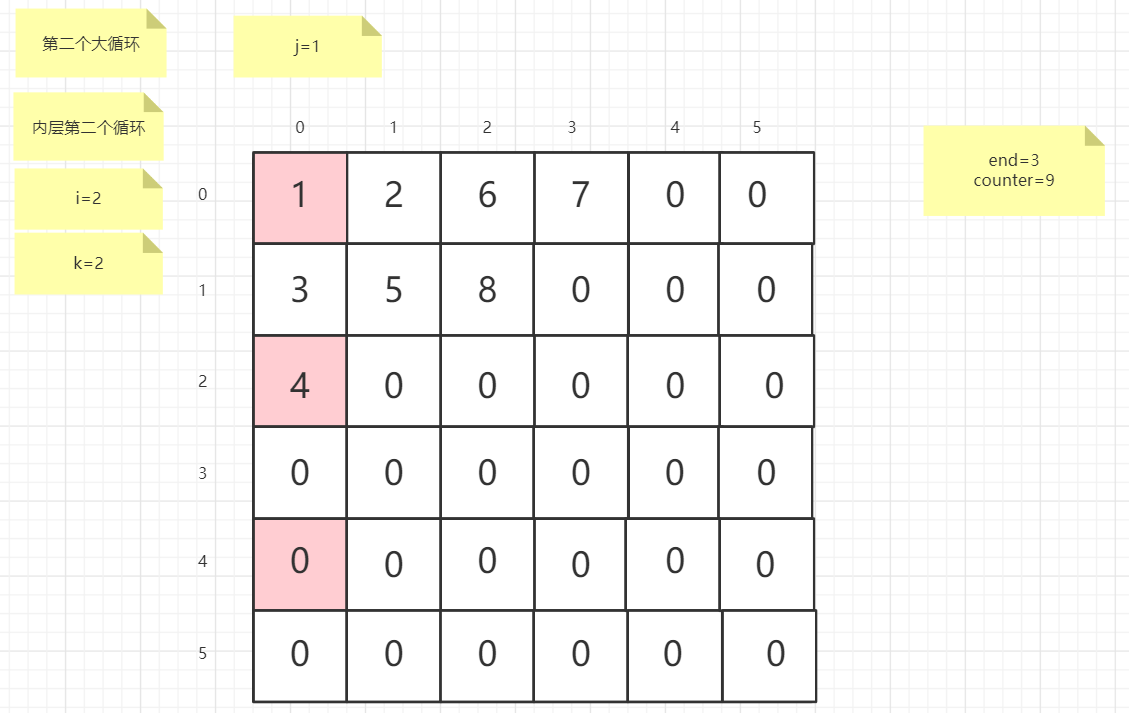
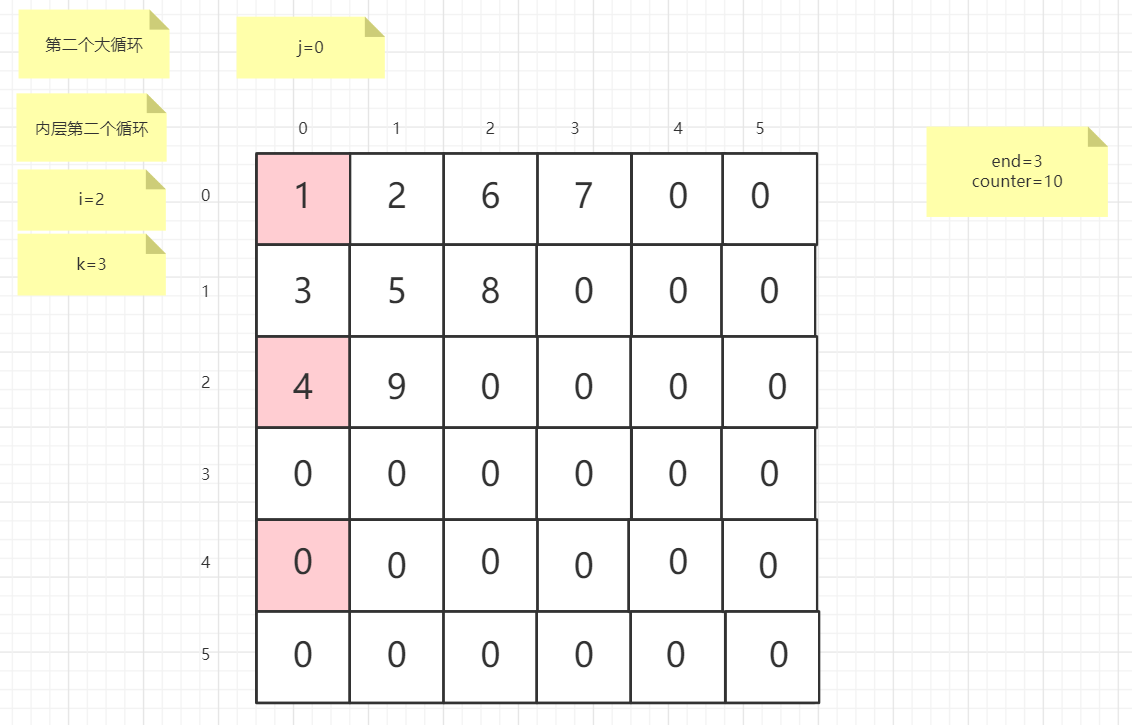
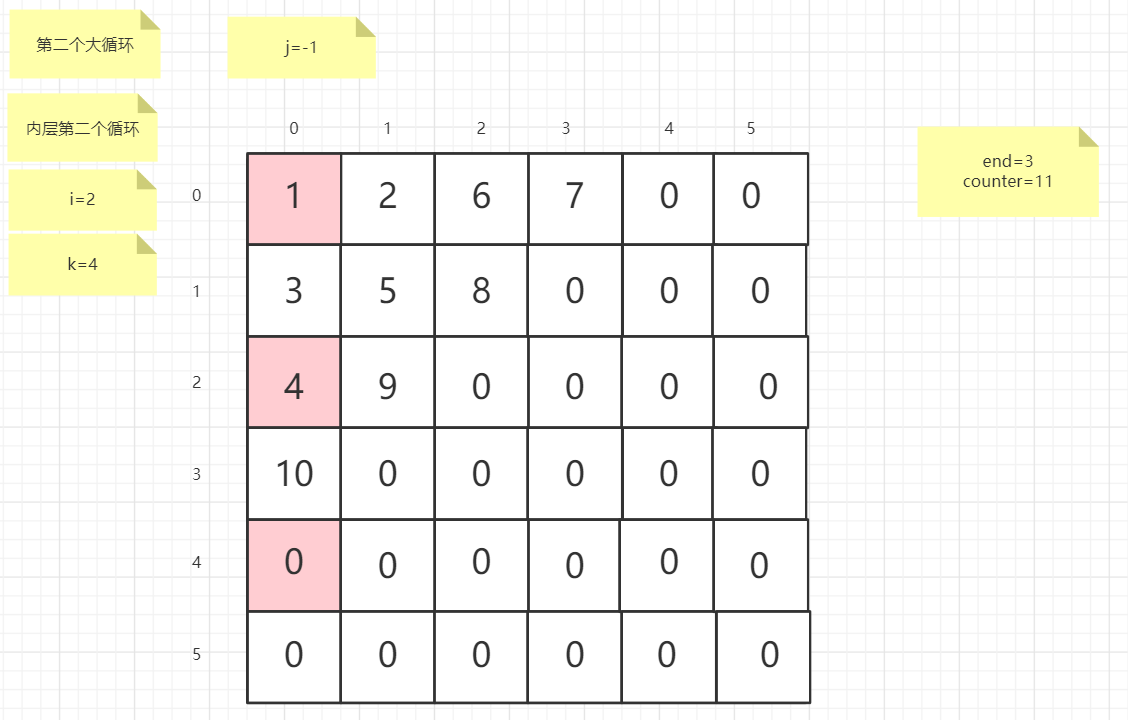
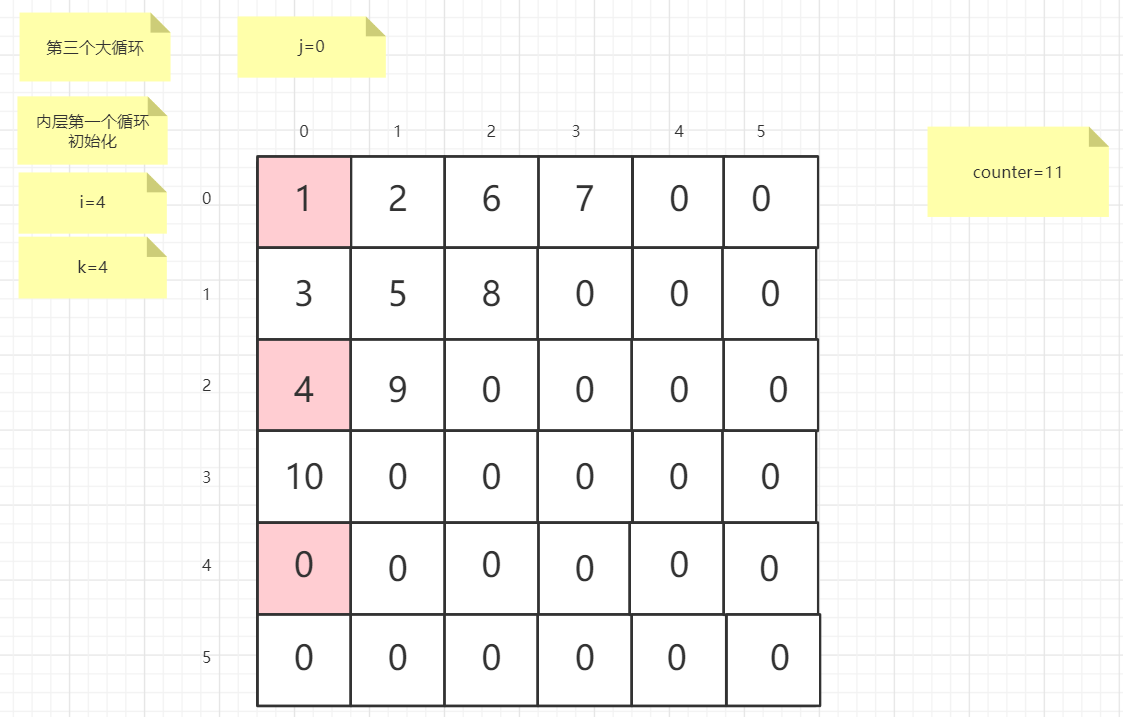
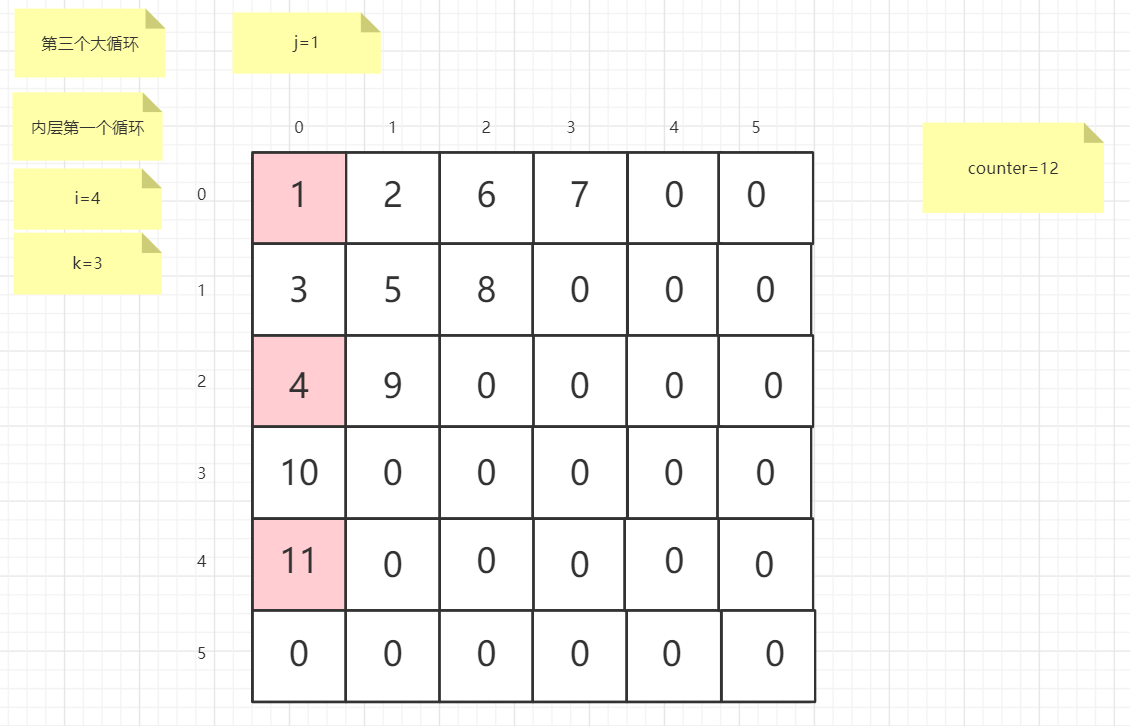
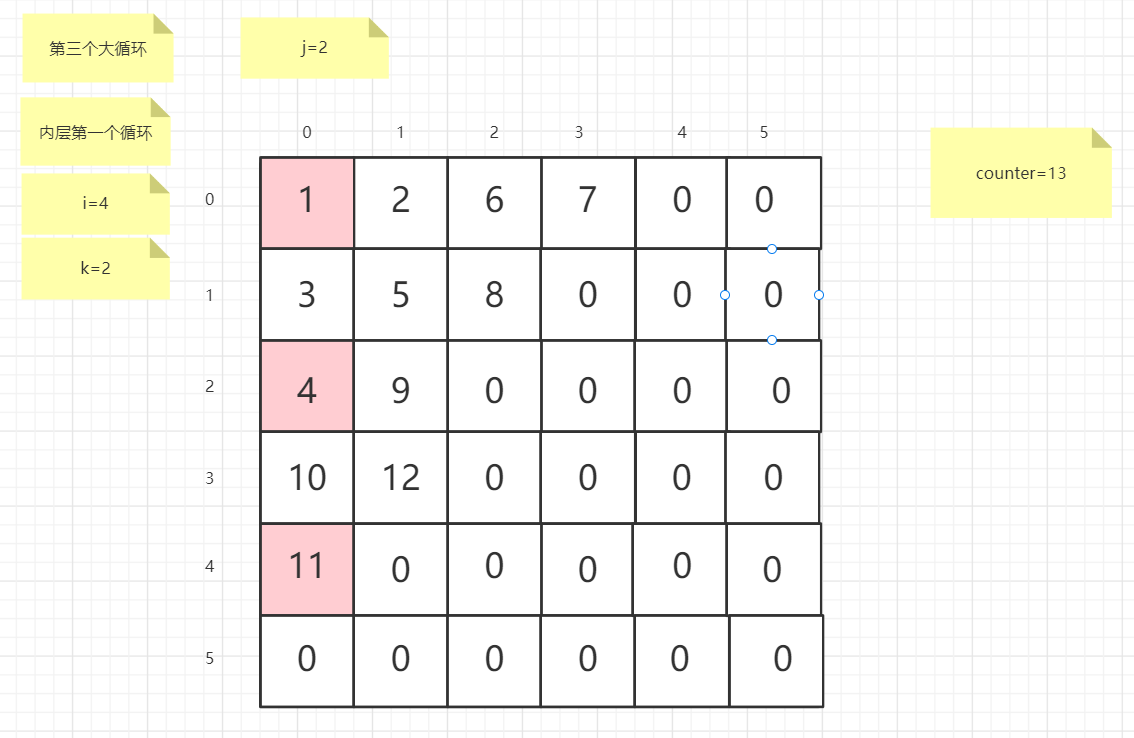
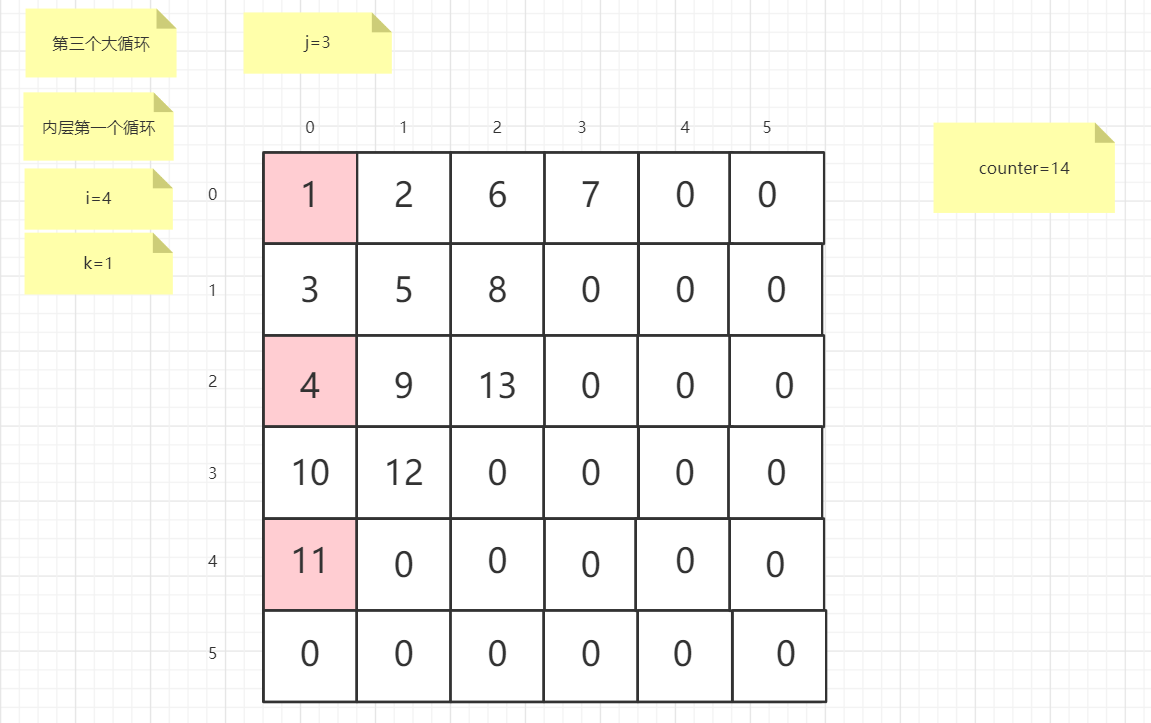
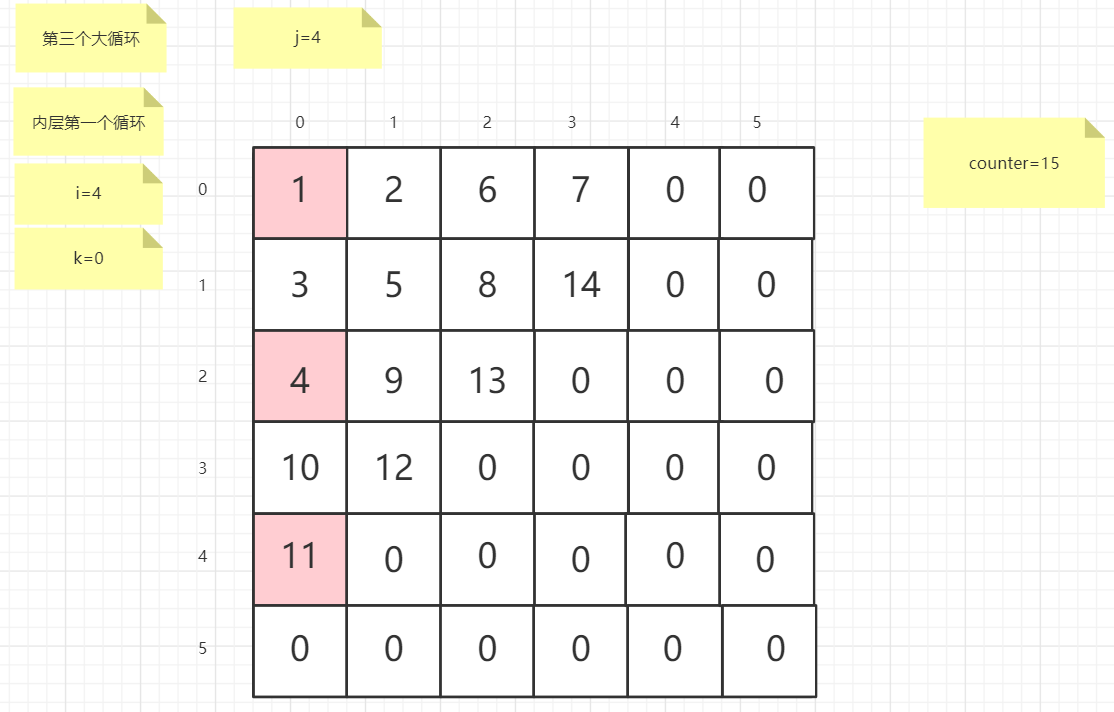
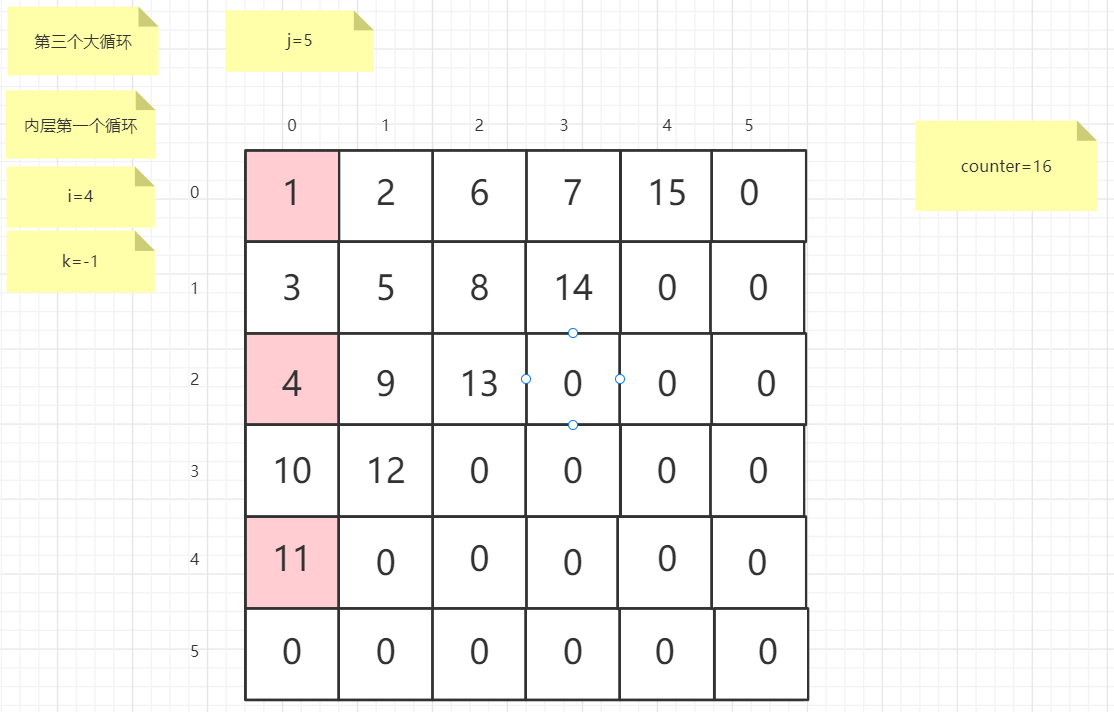
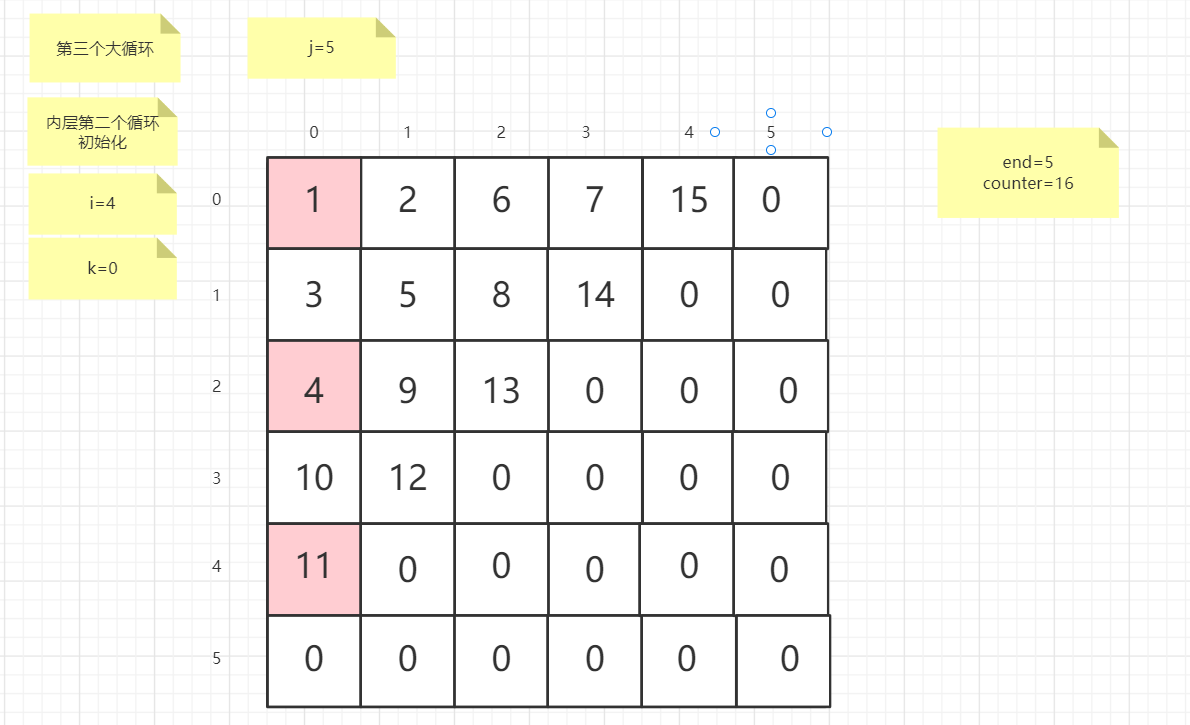
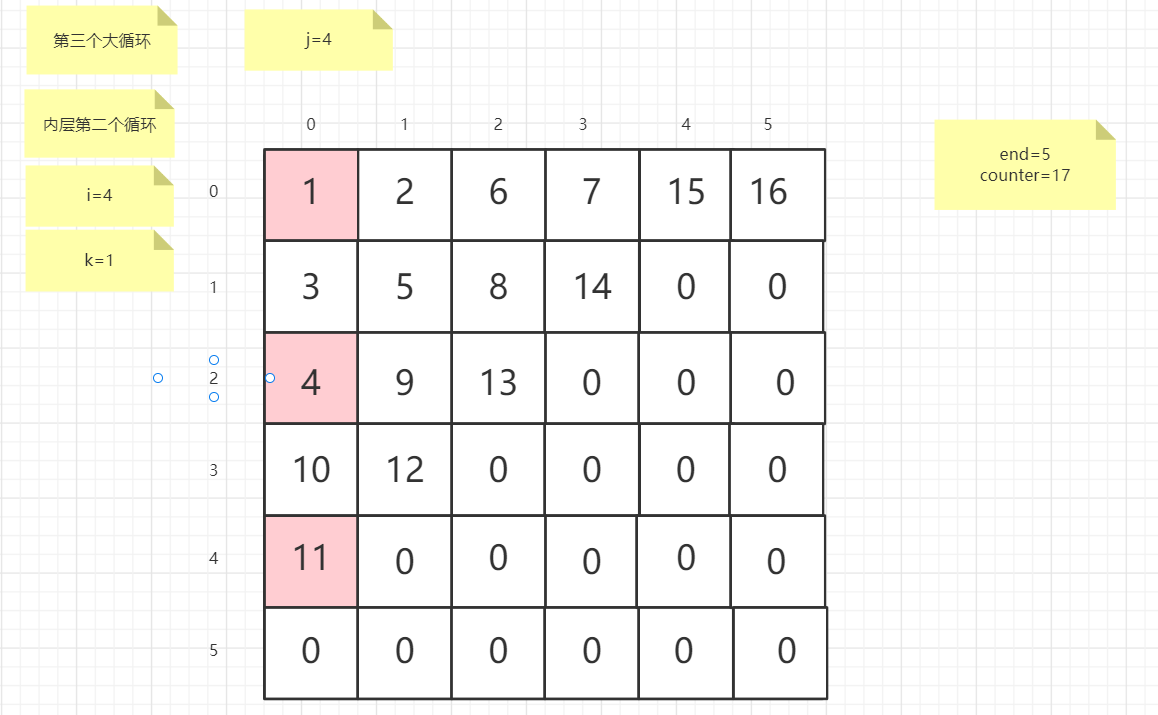
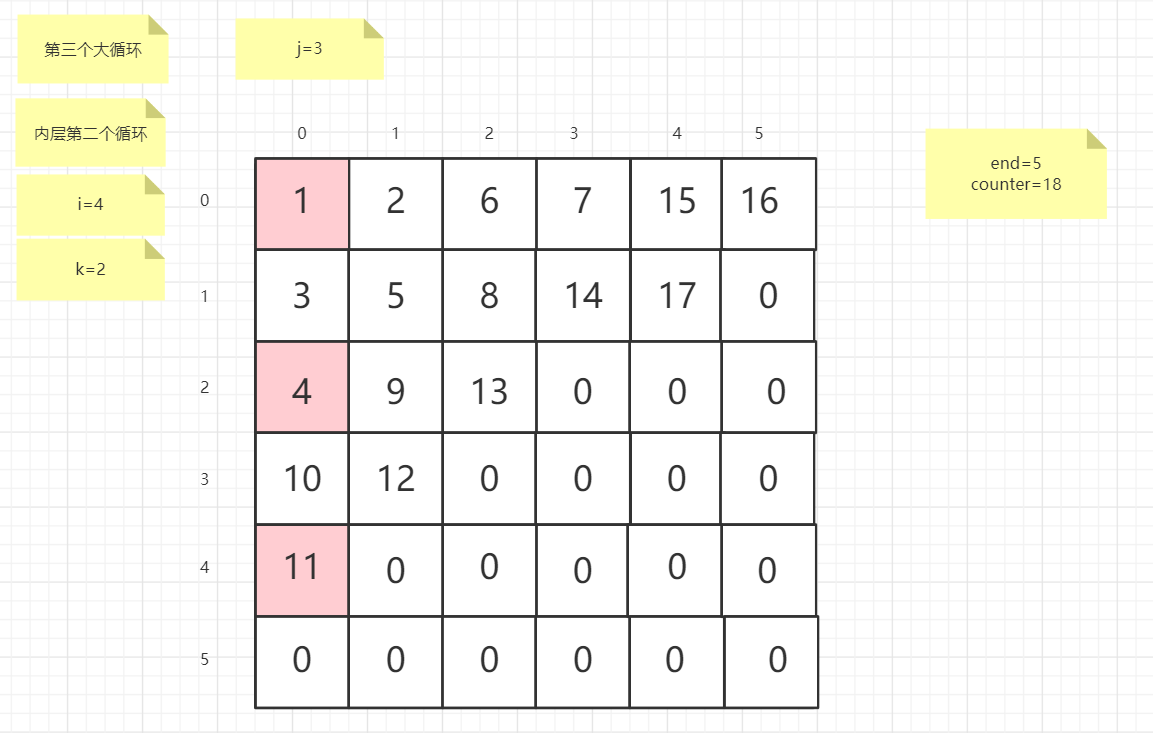
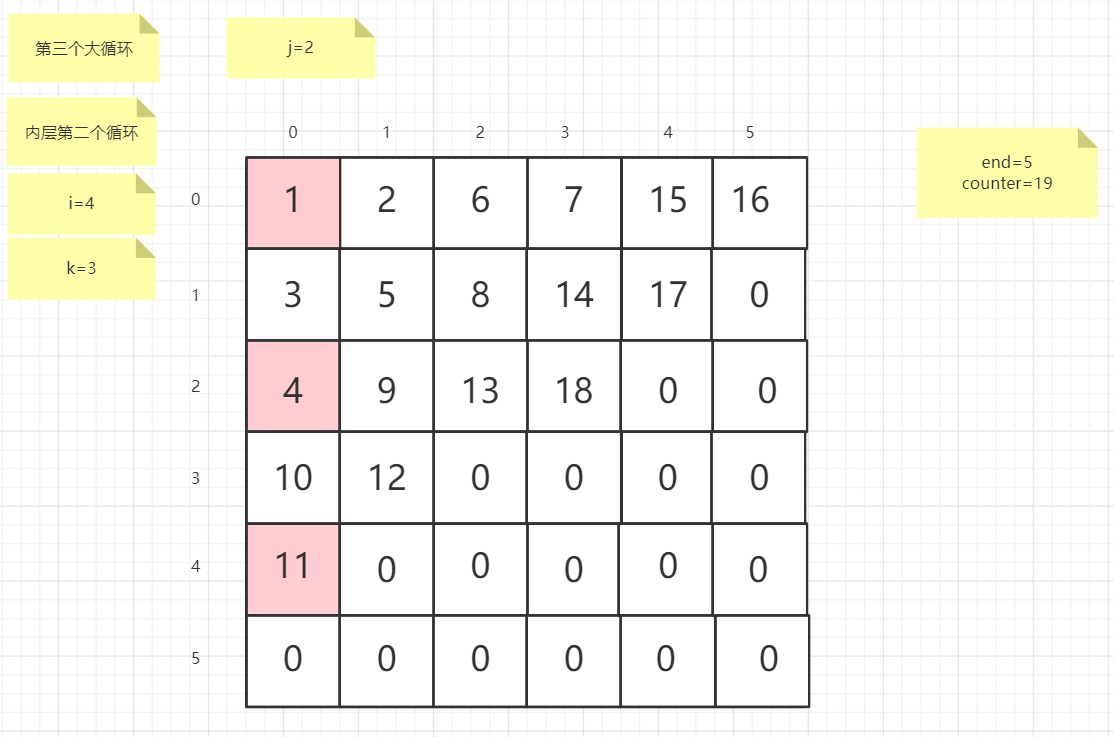
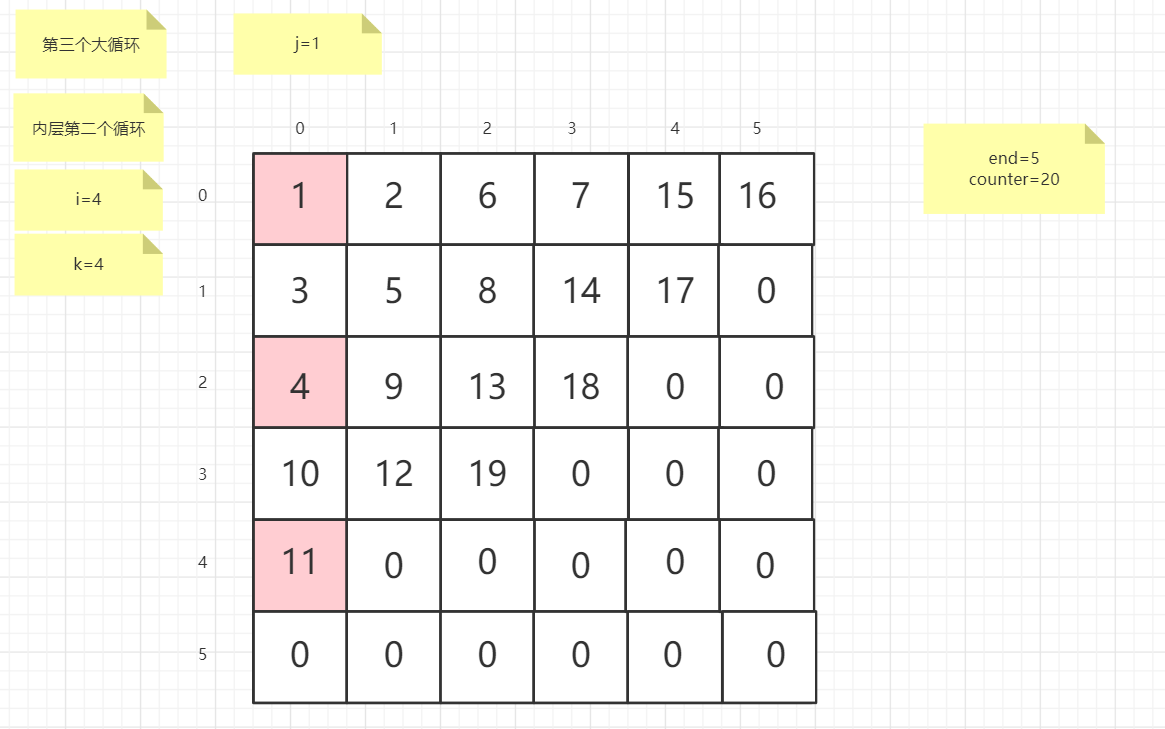
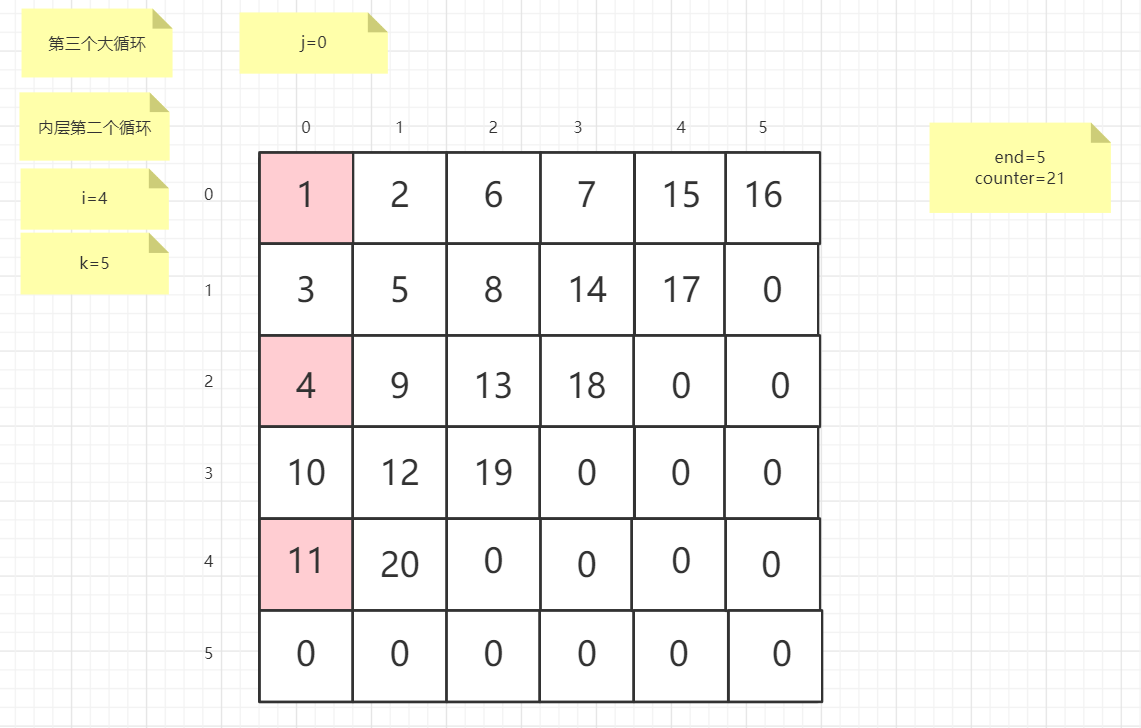
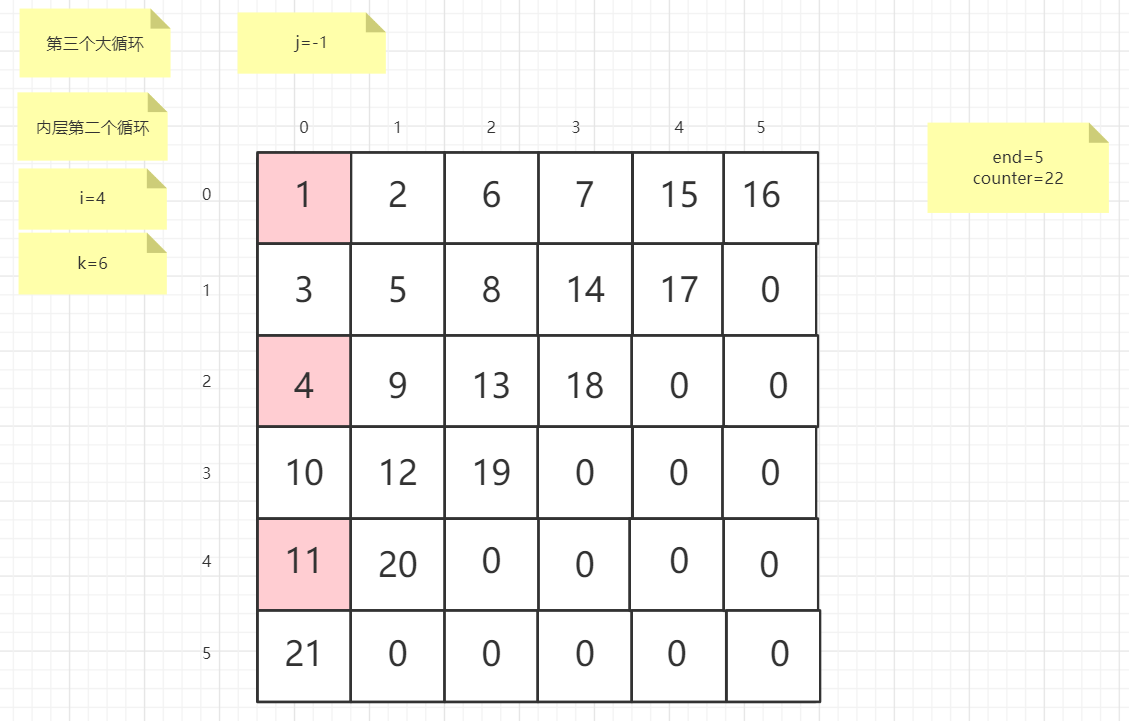
示例代码
1 | // i记录了次数和每一次输出开始的点的row |
连续法
把这些路径当作是连续的
维护一个[rowIndex,columnIndex]来走这一条连续的路径
示例代码
1 | int row = matrix.length; |

