全排列
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
1 | 输入:nums = [1,2,3] |
示例 2:
1 | 输入:nums = [0,1] |
示例 3:
1 | 输入:nums = [1] |
提示:
1 <= nums.length <= 6-10 <= nums[i] <= 10nums中的所有整数 互不相同
Related Topics
- 数组
- 回溯
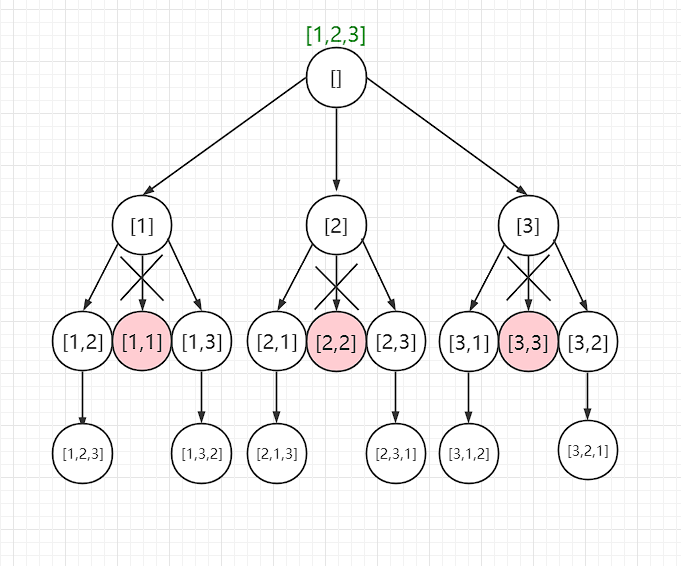
回溯
全排列,这是很经典的一道回溯的问题
回溯三要素
1、路径:已经做出了哪些选择
2、选择列表:可以选择的元素集合
3、结束条件:到了决策树的叶子节点处了
图示:
示例代码
1 | class Solution { |
所有的回溯问题,其实就是一棵决策树的遍历过程
在前序位置做出选择,在后序位置撤销选择

