区间问题
区间问题是什么,其实就是给了你一组区间,比如[[2,6],[9,13],[6,8],[1,4],[3,5],[9,11]]
然后让你有多少区间是被覆盖的,合并所有可以合并的区间等等操作
这种题目就两个步骤
第一步排序,按照左边界升序排序,右边界降序排序
第二步画图,画出两个边界之间的关系的所有可能的情况
1288.删除被覆盖的区间
然后我们按照以上两个步骤来解决这道题
排序
以[[2,6],[9,13],[6,8],[1,4],[3,5],[9,11]]作为测试数据
将其按照左边界升序排序,右边界降序排序后
变为[[1,4],[2,6],[3,5],[6,8],[9,13],[9,11]]
用图像来表示就是这样
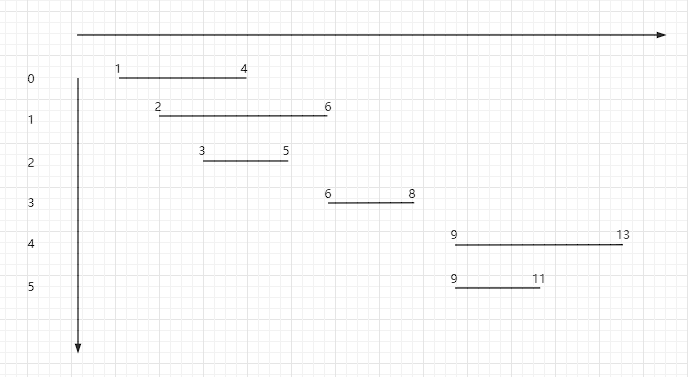
画图
然后我们来画图将所有出现的区间关系画出来
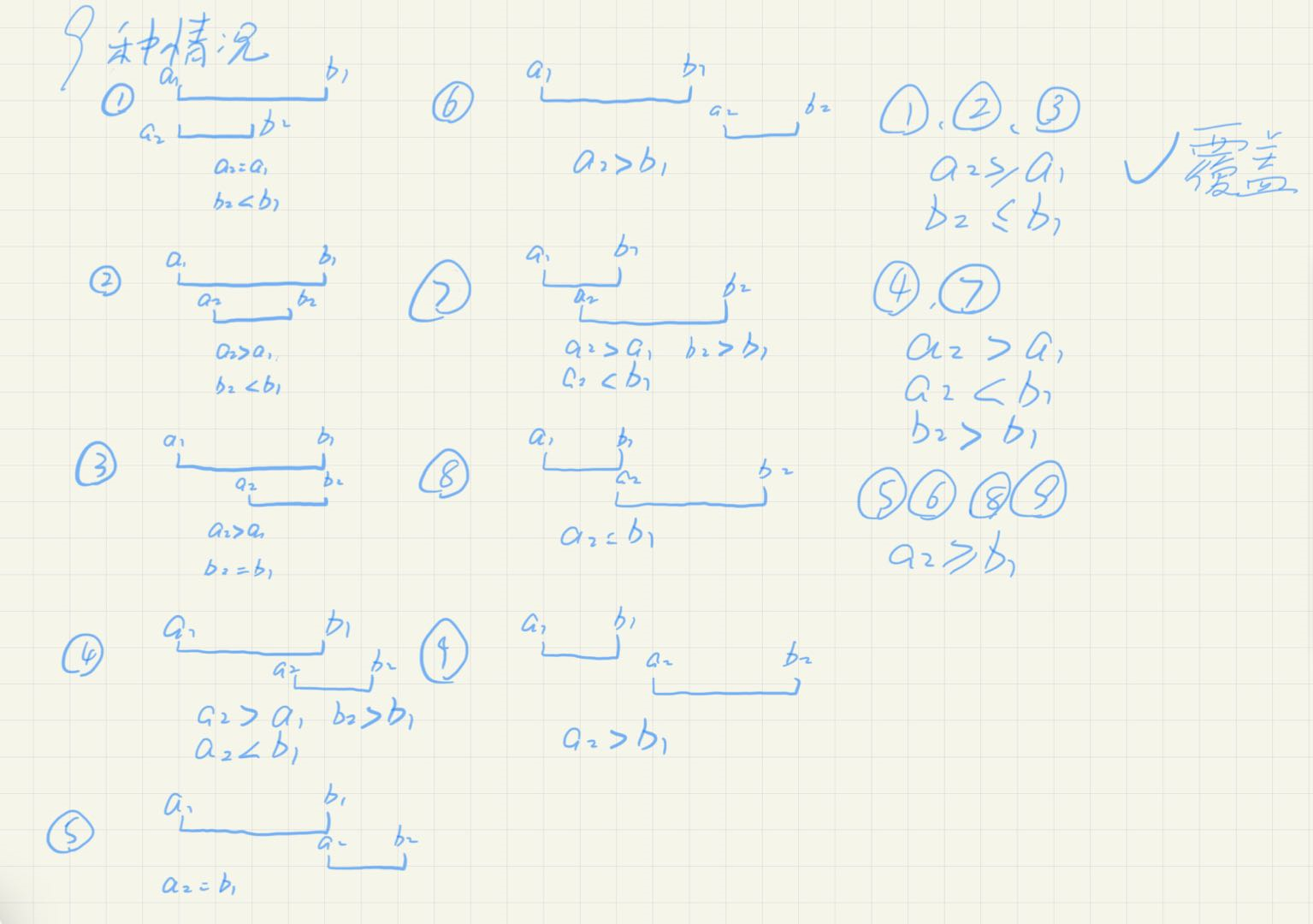
其中①②③这三种情况都是属于覆盖的情况,所以我只要将这些情况记录到res中,最后intervals.length-res就是需要删除的被覆盖的区间个数
④⑦都是属于区间相交的情况
⑤⑥⑧⑨属于区间交错的情况
心中有图,代码我有!
1 | class Solution { |
56.合并区间

这一题也是按照上述两个步骤做就行了,这里直接上代码
1 | class Solution { |
或者使用以下的方法
1 | class Solution { |
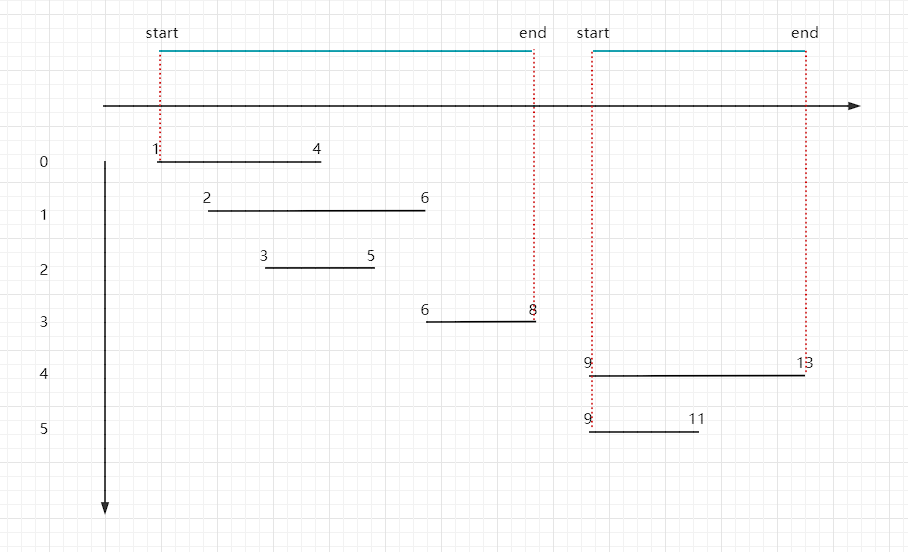
986.区间列表的交集

这道题和上述思路一致的,只需要将交集的部分放入res中
1 | class Solution { |

