解数独
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
- 数字
1-9在每一行只能出现一次。 - 数字
1-9在每一列只能出现一次。 - 数字
1-9在每一个以粗实线分隔的3x3宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 '.' 表示。
示例 1:

1 | 输入:board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]] |

提示:
board.length == 9board[i].length == 9board[i][j]是一位数字或者'.'- 题目数据 保证 输入数独仅有一个解
Related Topics
- 数组
- 回溯
- 矩阵
回溯
这里需要关注一下题目给的提示,我们来一一分析
第一条和第二条告诉我们,传入的数组是一个固定9 * 9的矩阵
第三条告诉我们'.'指的是空位
第四条告诉我们题目传入的数独只有一个答案,这就代表着我最后穷举出来解满足条件的只有一个

回溯三要素
1、路径:填上的数字,就是棋盘上的数字
2、选择列表:'1'-'9'
3、结束条件:穷举到最后一个格子(由第四条提示可得)
下面直接上代码
1 | class Solution { |
我们来看下这个valid函数中判断九宫格内是否有重复数字的代码
1 | if (board[(row / 3) * 3 + i / 3][(column / 3) * 3 + i % 3]==key){ |
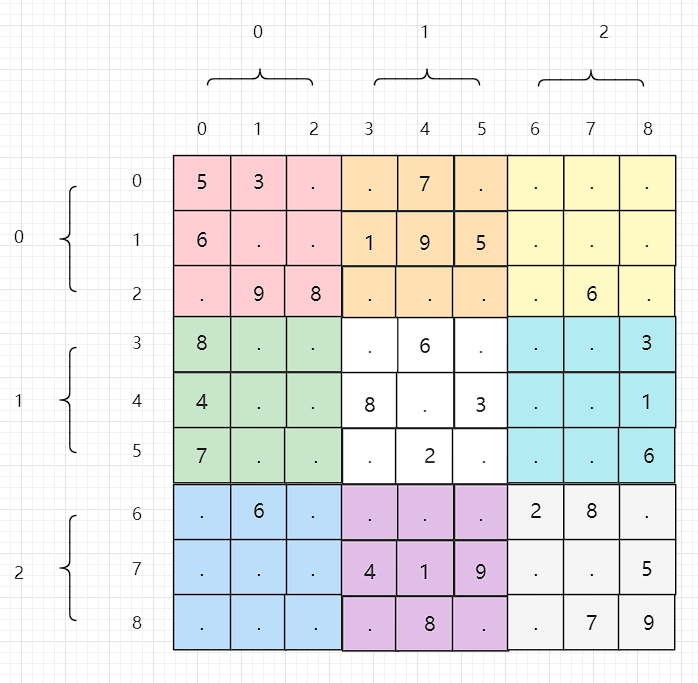
1 | row/3 可以将其映射到其对应的九宫格行 |
进阶
如果我将提示的第四条,即只有一个正确答案这个条件删除,那这道题该怎么做?
其实也不难,只要改变结束条件即可,上述代码是直接将可以穷举到最后的答案返回
因为题目说了只有唯一解,所以我不需要再对其进行判断
既然删除了只有唯一解这个条件,那我就要对穷举到最后的答案进行验证
怎么验证呢,那就是验证每一行每一列对角线加起来都是一样的
1 | private boolean valid(int[][] board){ |

