N皇后
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
1 | 输入:n = 4 |
示例 2:
1 | 输入:n = 1 |
提示:
1 <= n <= 9
Related Topics
- 数组
- 回溯
回溯
N皇后问题和全排列问题被称为回溯问题的两大经典问题
今天我们就来盘一盘N皇后问题
回溯题目三大基本元素
路径、选择列表、结束条件
我们来一 一看看在这道题目中都和什么对应
路径
路径就是已经选择将皇后放哪后的棋盘board
选择列表
选择列表就是每一行的每一列放QUEUE
结束条件
结束条件就是当选择到了最后一行,则将当前棋盘加入到结果集中去
下面上代码
1 | class Solution { |
以下是 n=4 的递归树
黄色的小方块表示此次选择是合法的
红色的小方块表示此次选择是不合法的,直接跳过此次选择
绿色的屏障表示的此次选择到了结束条件,直接将其放入结果集中
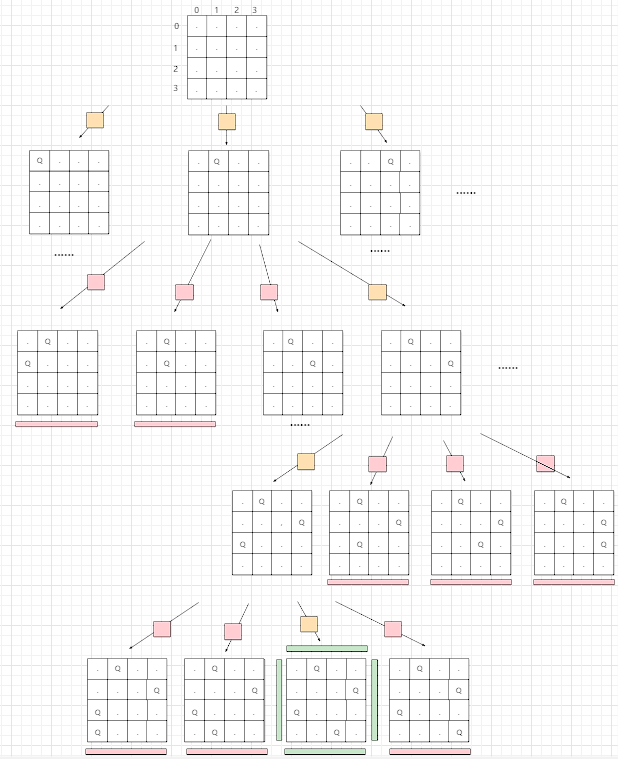
回溯问题无非就是遍历一颗递归树,然后在前序位置判断这次选择是否合法,如果合法就进入子树,然后在后序位置将此次选择撤销

