括号生成
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例 1:
1 | 输入:n = 3 |
示例 2:
1 | 输入:n = 1 |
提示:
1 <= n <= 8
Related Topics
- 字符串
- 动态规划
- 回溯
回溯
直接穷举所有情况
1 | public List<String> generateParenthesis(int n) { |
这种方法的递归树会很大
原因在于修剪的力度不够大,canAdd只能判断当前的index位是否可以加入choice
但是无法保证最后生成的字符串是符合左右括号数目相等的
所以需要在满足推出条件的时候,再次判断是否符合左右括号数目一致
原因在于我无法根据已作出选择的左右括号数量来判断最后是否合法
换下思路,用左右括号的剩余数量就可以来判断最后是否合法,只要right>=left即可
代码优化
1 | public List<String> generateParenthesis(int n) { |
这里给出优化后 n=2 的递归树
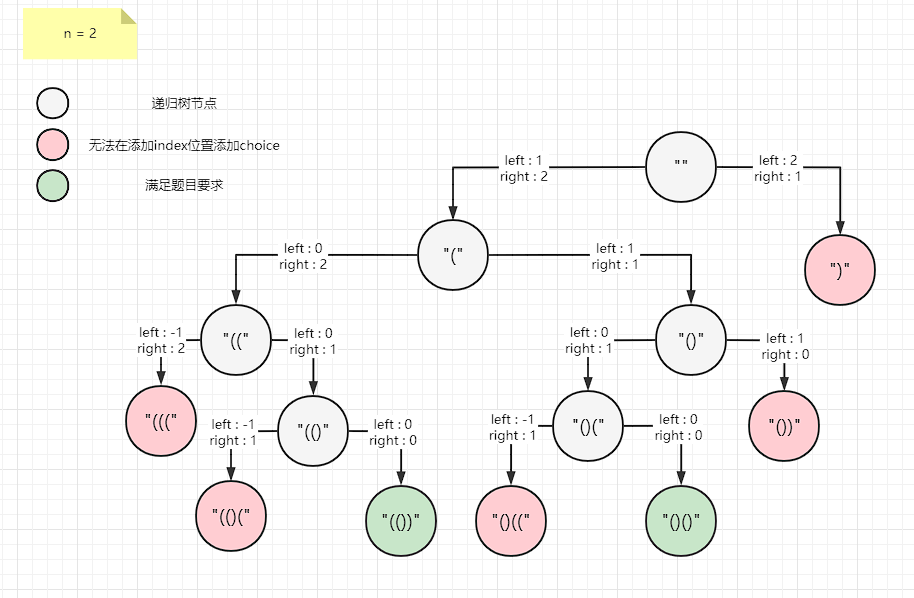
优化前的 n=2 的递归树
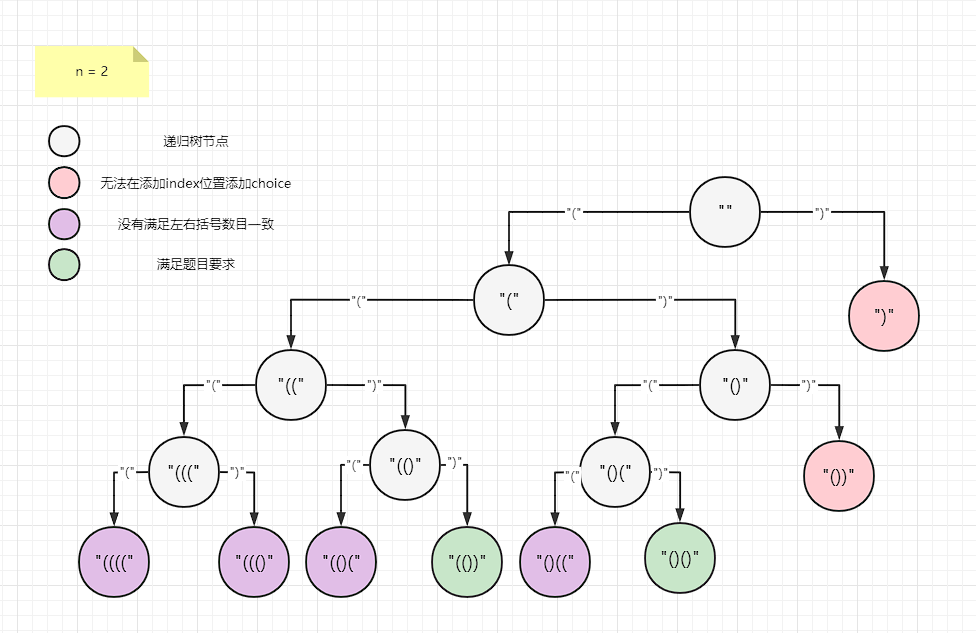
n=2 看不出优化后明显的增加修剪的力度
感兴趣的可以自己画一画 n=3 的递归树,你就会发现有很明显的区别

