最后K个数的乘积
请你实现一个「数字乘积类」ProductOfNumbers,要求支持下述两种方法:
1. add(int num)
- 将数字
num添加到当前数字列表的最后面。
2. getProduct(int k)
- 返回当前数字列表中,最后
k个数字的乘积。 - 你可以假设当前列表中始终 至少 包含
k个数字。
题目数据保证:任何时候,任一连续数字序列的乘积都在 32-bit 整数范围内,不会溢出。
示例:
1 | 输入: |
提示:
add和getProduct两种操作加起来总共不会超过40000次。0 <= num <= 1001 <= k <= 40000
Related Topics
- 设计
- 队列
- 数组
- 数学
- 数据流
法一:暴力
这题很好理解,但是如果想要写出一个复杂度低的算法不是一件简单的事情
下面我们先来用最简单最通俗易懂的方法来实现
因为数组长度不定,所以使用source用来存储原数组
返回最后k个数字的乘积getProduct,那我只需要遍历source的最后k个数字并将其相乘返回即可
1 | public class ProductOfNumbers { |
好,没有问题,提交!
但是Medium的题目会这么简单吗?NO!
只有通过大测试数据,算法才算通过
这种简单的算法,虽然好想,但是扛不住大数据,接下来介绍一种新解法
法二:前缀积
在看这个之前,最好先了解过前缀和的知识,可以移步这篇文章【303-Easy】区域和检索-数组不可变
且听我解释各变量的作用,再看代码
source和之前的作用是一样的,是用来存储原数组的
size就是原数组的长度
zeroIndex代表的是 0 最后一次出现的位置
preMultiply的作用是存储前缀积的结果的,但是这里的preMultiply和之前的前缀和的定义略有不同
这里preMultiply.get(i)的定义是
i > zeroIndex
原数组在[zeroIndex+1,i]的累乘
i < zeroIndex
无定义
1 | public class ProductOfNumbers { |
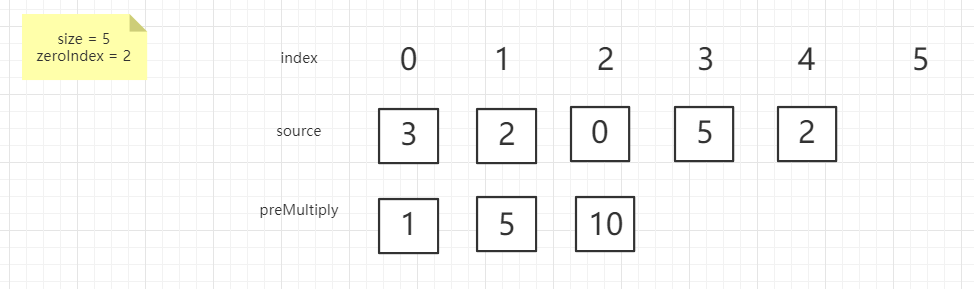
图解
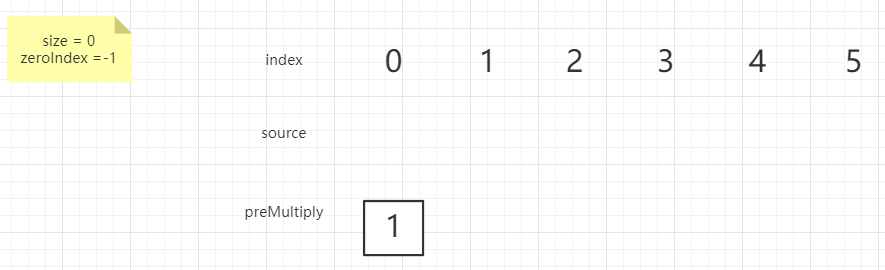
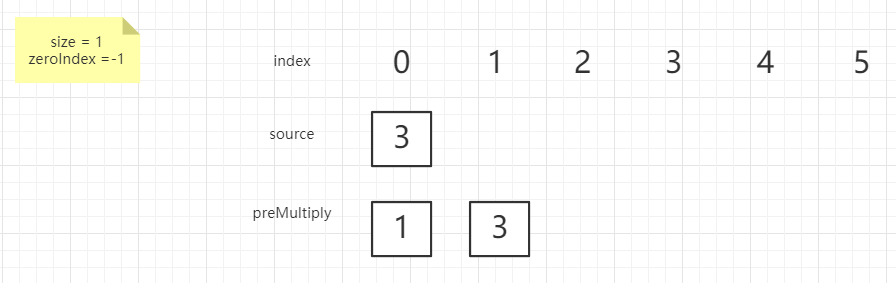

这一步比较特殊,当我出现了 0 的时候所有的前缀积都无效了,所以直接清除,然后记录 0 出现的位置
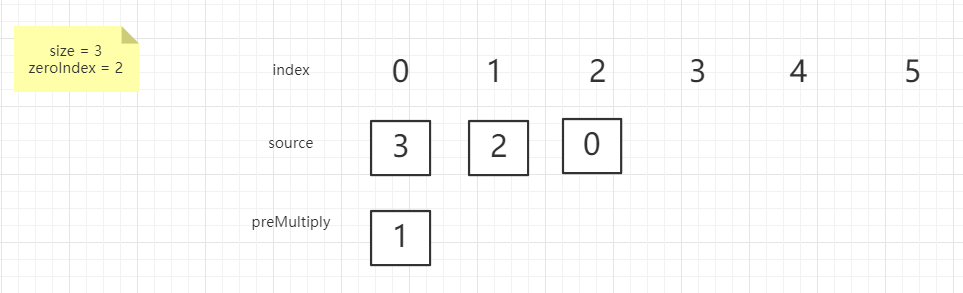
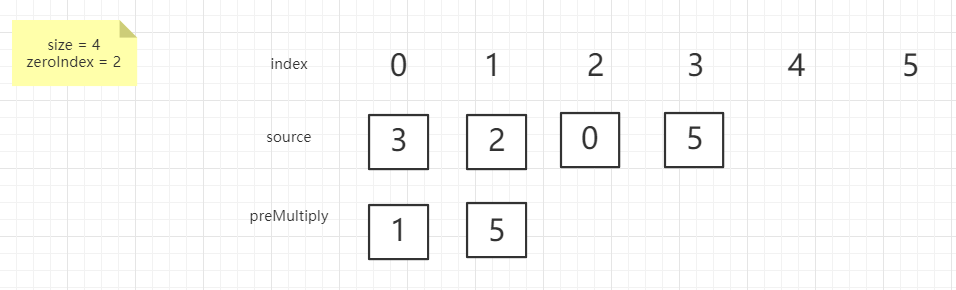
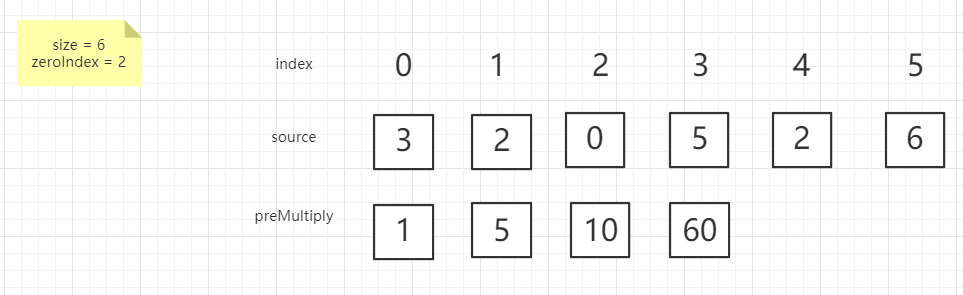
接下来解释一下代码
1、构造函数

构造函数做的事就是初始化一些变量,这些变量的意义前面讲述过了这里就不赘述了
2、add函数

首先将其直接放入source集合中
接下来对于不同的num做出不同的处理
num为 0
重置前缀积集合,即清空集合,并放入 1
更新zeroIndex
(这里直接将size赋值给zeroIndex的原因是size是方法结束之后才自增的,自增前的size表示的就是当前元素的索引)
num不为0
更新前缀积集合,这里的size-zeroIndex-1需要理解(这里我当时是通过画图推敲得知)
我的理解就是将当前值乘以原数组 0 之后的所有数的乘积得到的值放入前缀积
3、getProduct函数
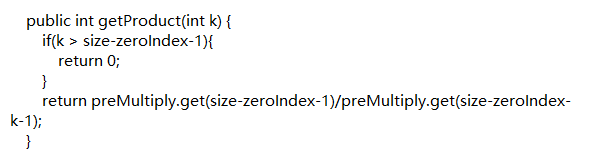
size-zeroIndex-1就是原数组 0 之后有几个数字
如果这个数字比 k 小,则可以直接返回 0
不然,则返回preMultiply.get(size-zeroIndex-1)/preMultiply.get(size-zeroIndex-k-1);
preMultiply.get(size-zeroIndex-1)是原数组在 0 之后所有数字的乘积
preMultiply.get(size-zeroIndex-k-1)是原数组在 0 之后所有数字,倒数第 k 个数到 0 后第一个数的乘积
注:如果
size-zeroIndex-k-1为 0 ,则没有意义,就是 1 ,占位用的

