【64-Medium】最小路径和

发表于 | 分类于 ， | | 阅读量 次
字数统计: 1.1k

最小路径和

给定一个包含非负整数的 m x n 的网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

1
2
3
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

1
2
输入：grid = [[1,2,3],[4,5,6]]
输出：12

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 200
  • 0 <= grid[i][j] <= 100

分析：一般来说，遇到这种统计可行路径的数量，或者求最小路径的时候，使用动态规划和搜索这两种方法，但是搜索更适用于数据规模较小的题目

动态规划

动态规划算法，我们主要关注以下两点。

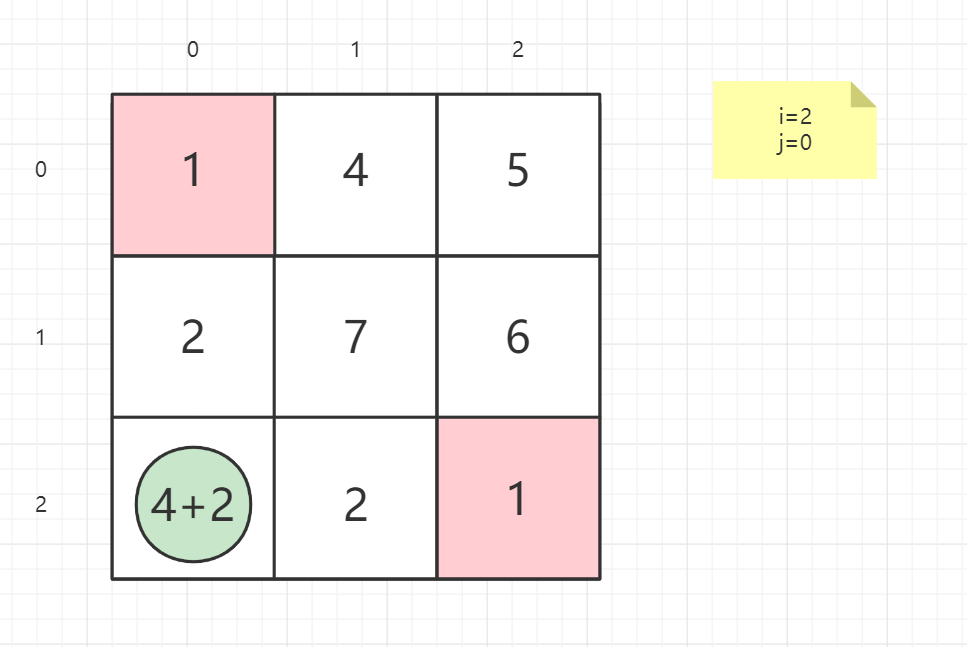
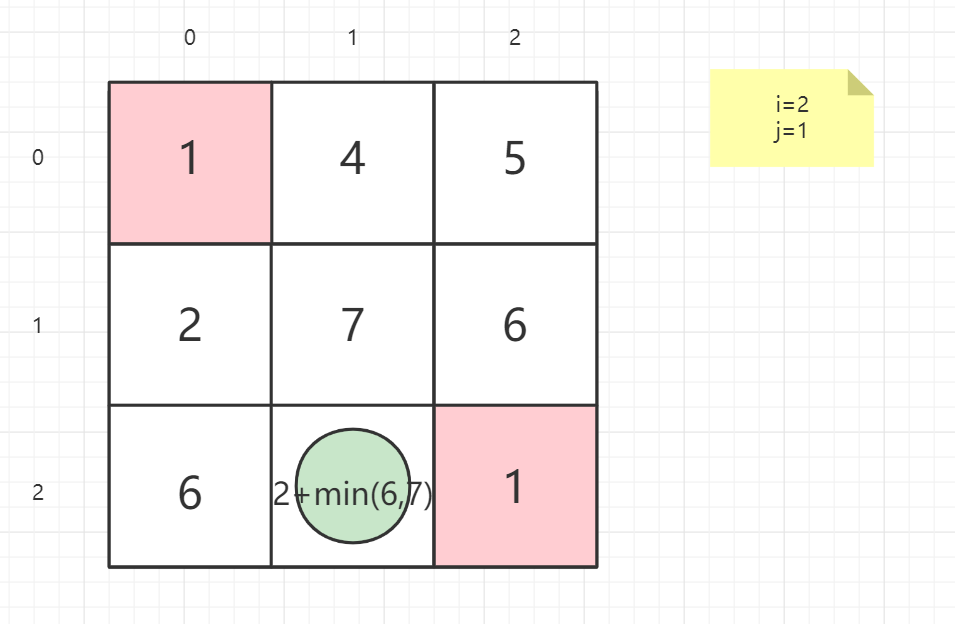
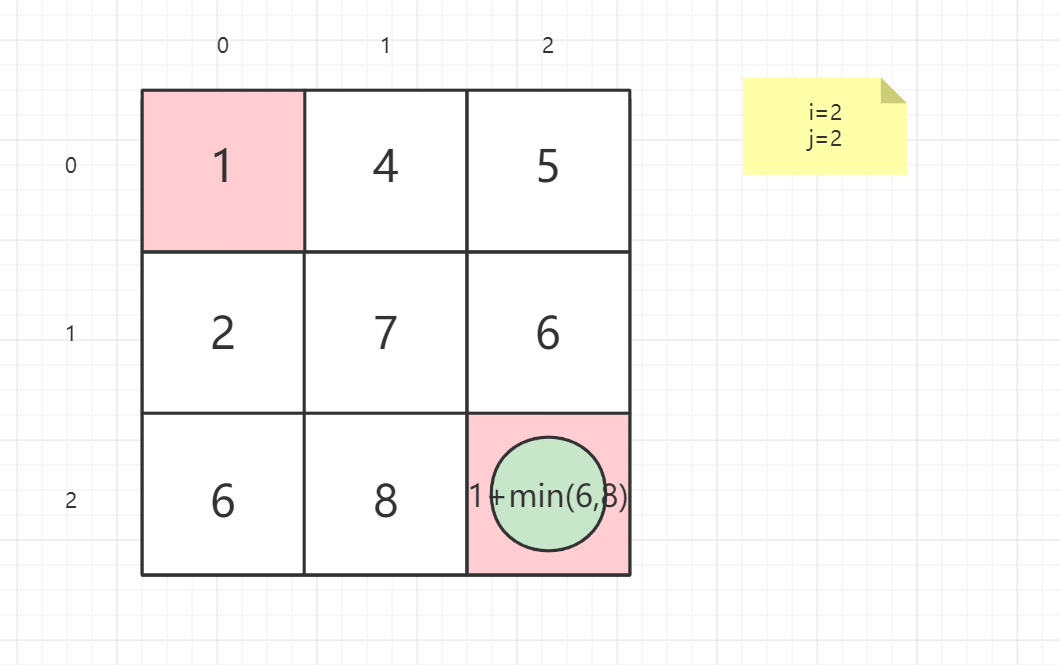
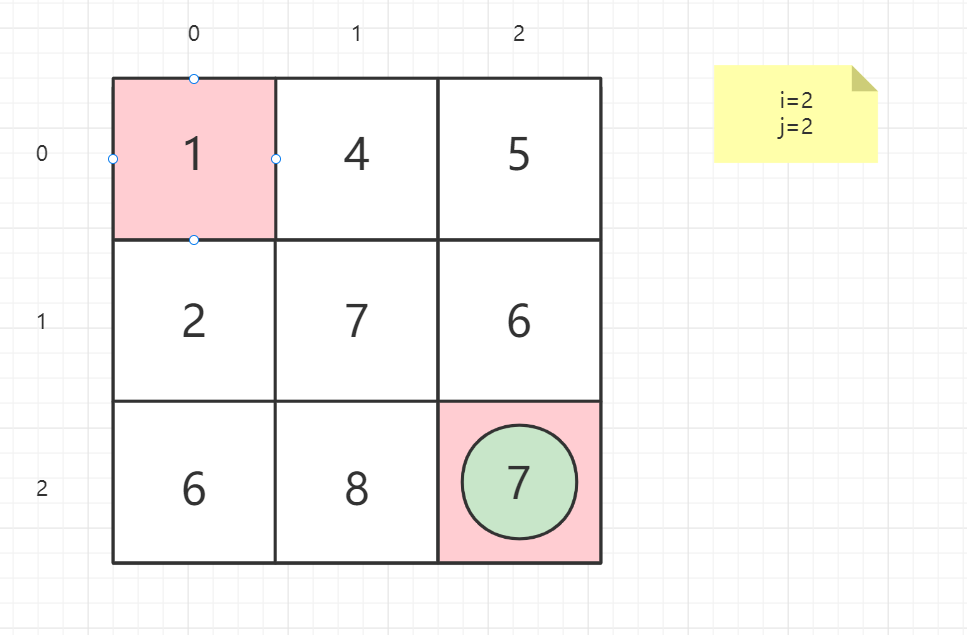
  1. 状态的设置。在这个题目里，由于要求最小路径和，我们可以令 dp[ i ] [ j ] 代表从（i，j）点走到右下角点的最小路径和。

  2. 状态转移方程。我们考虑如何来求出 dp [ i] [j]。由于每次只能往右或者下走，所以从（i，j）只能走到（i+1，j）或者（i，j+1)。换言之，dp[ i ] [ j ] 的前继状态只有dp[ i+1 ] [ j ], dp[ i ] [ j+1 ], 所以我们在两者取最小，然后加上这个格子内的数即可

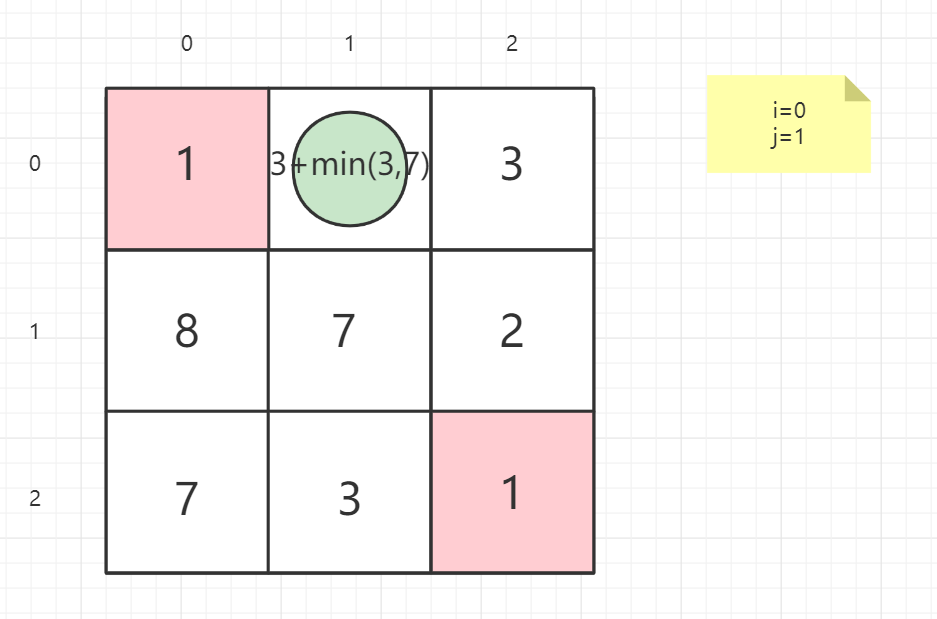
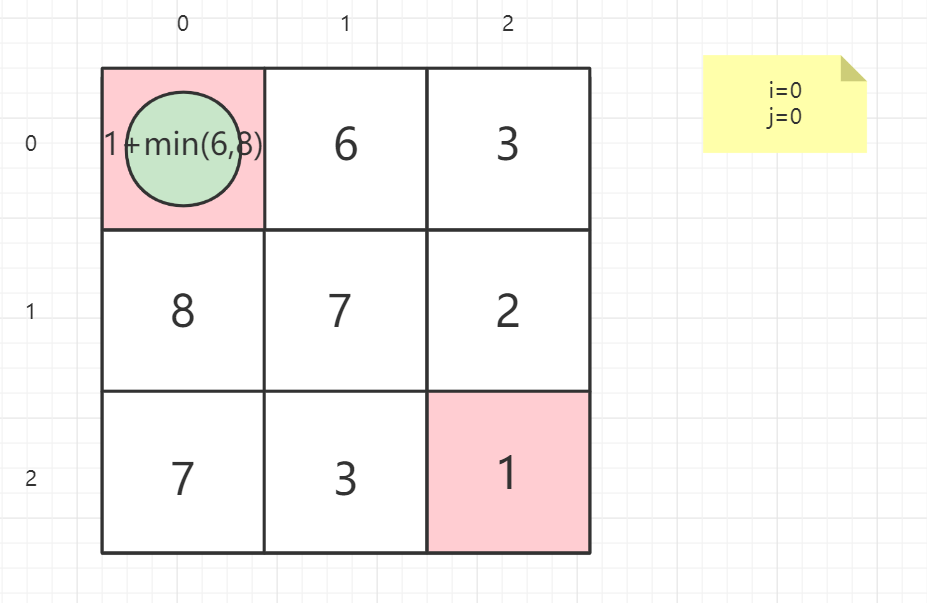
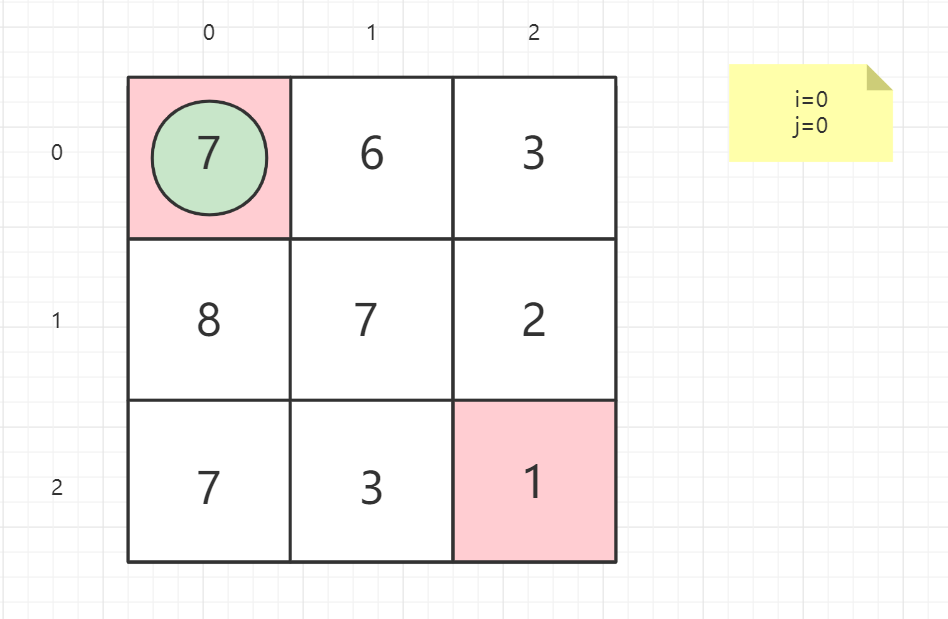
dp(i,j) = grid(i,j) + min(dp(i + 1,j),dp(i,j + 1))

是需要特殊处理的，当然还有终点元素也是要做个排除，下面先看流程图

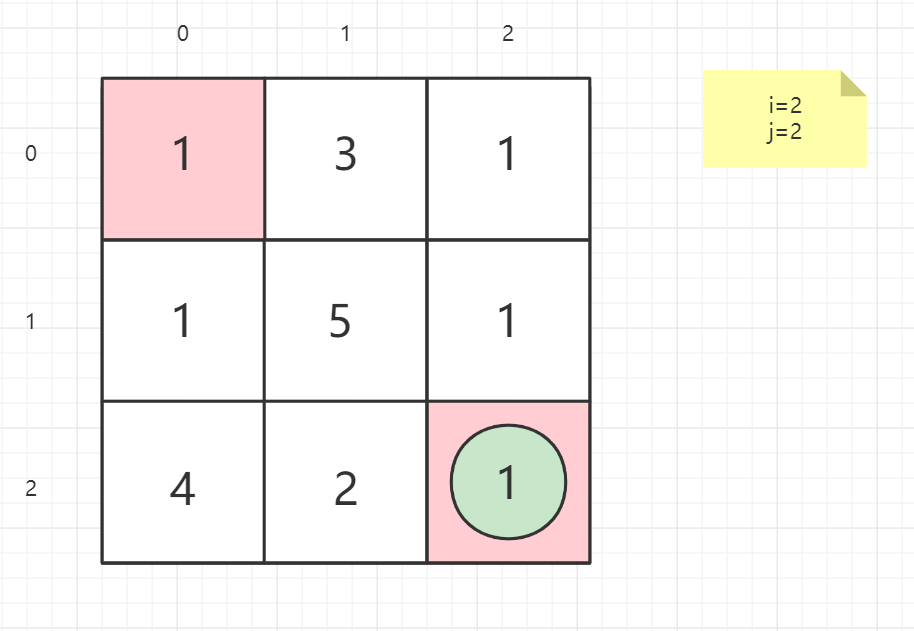
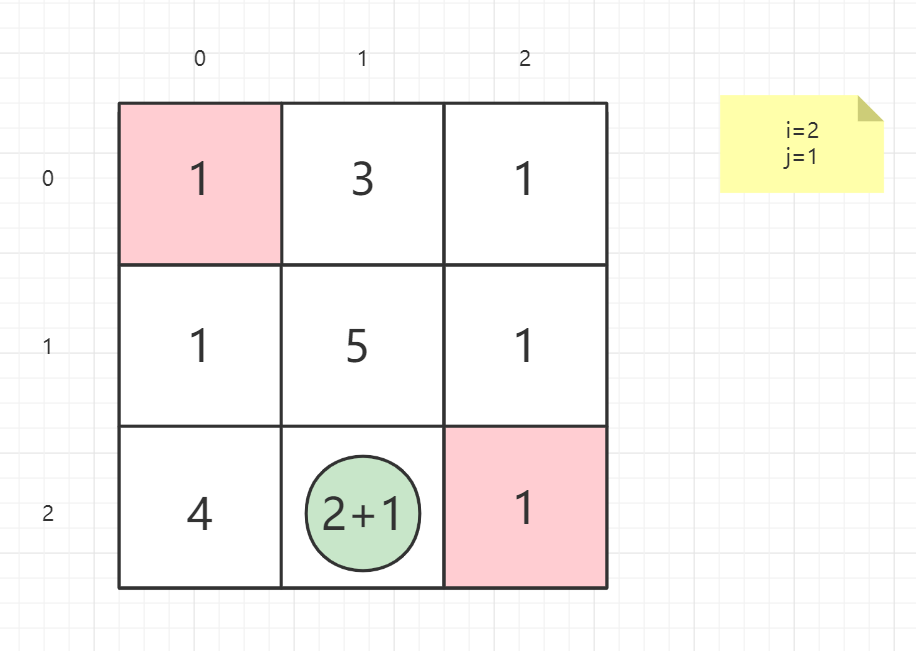
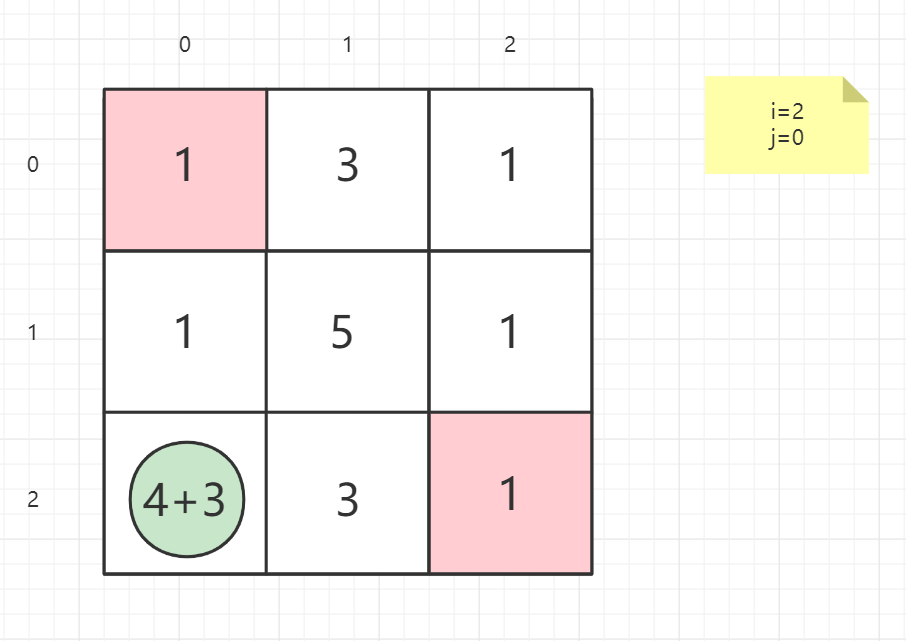
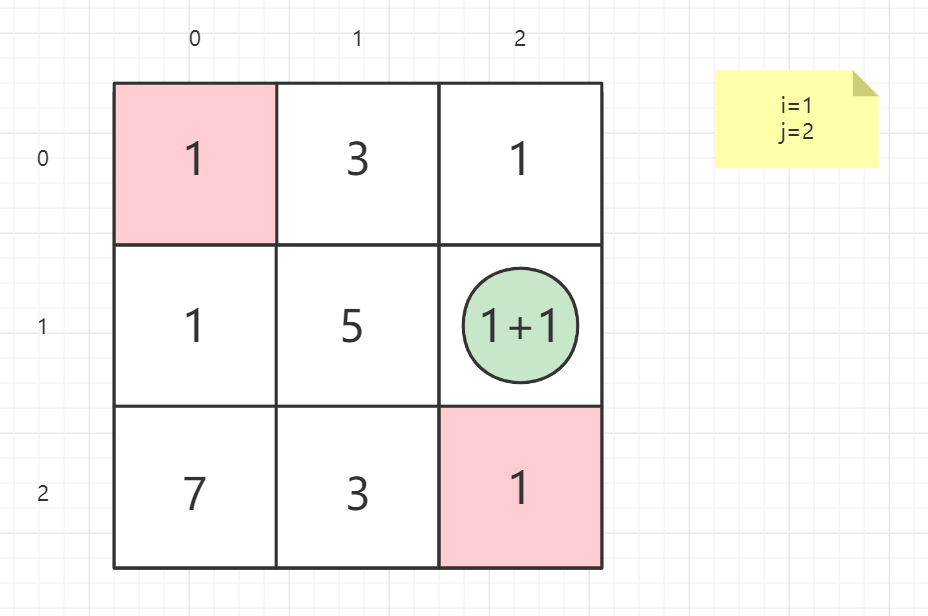
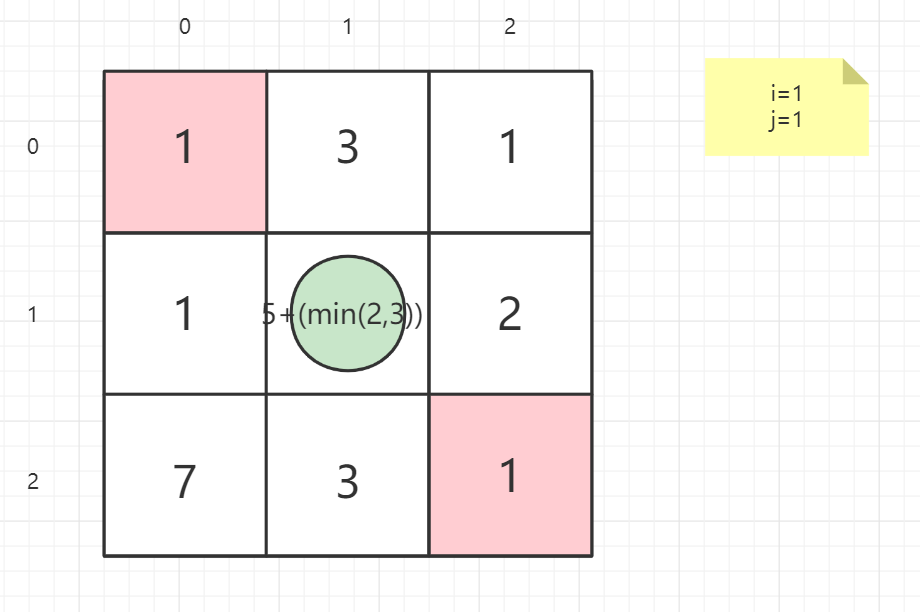
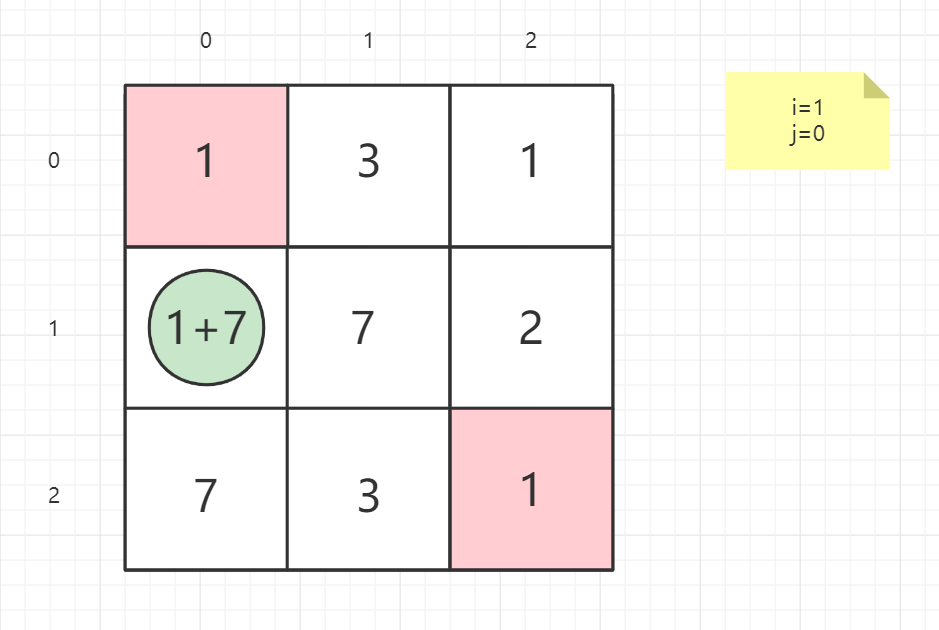
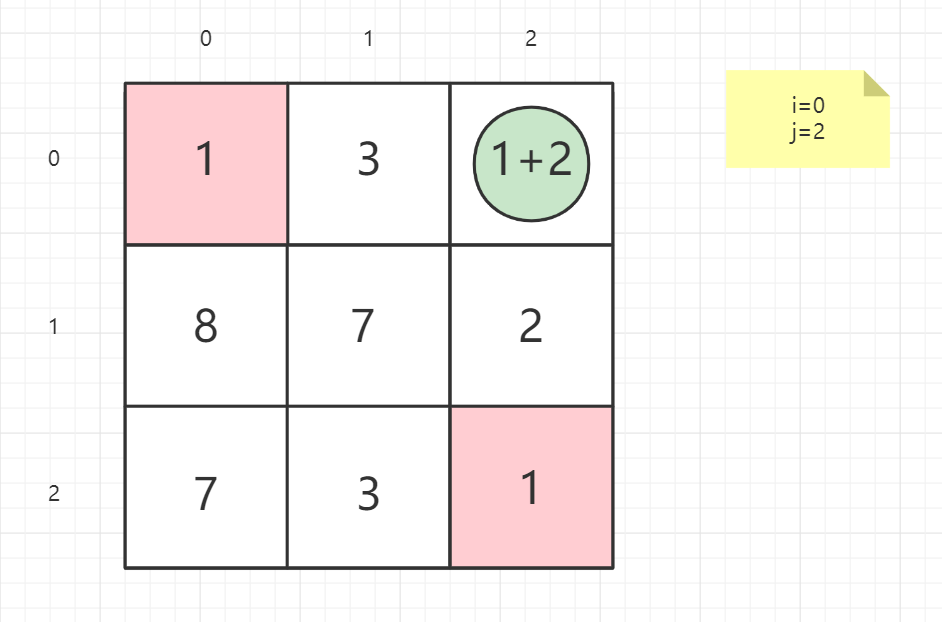
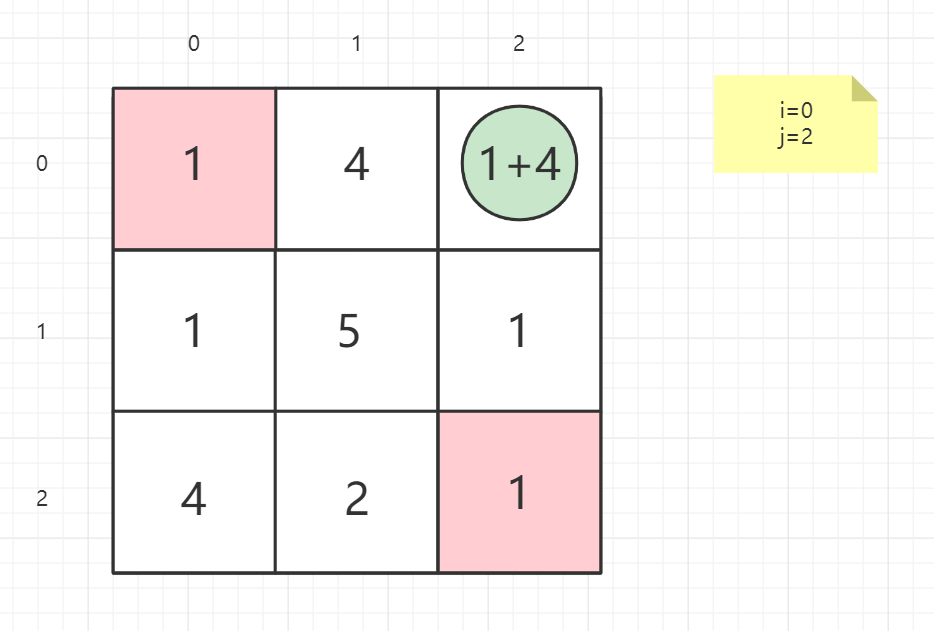
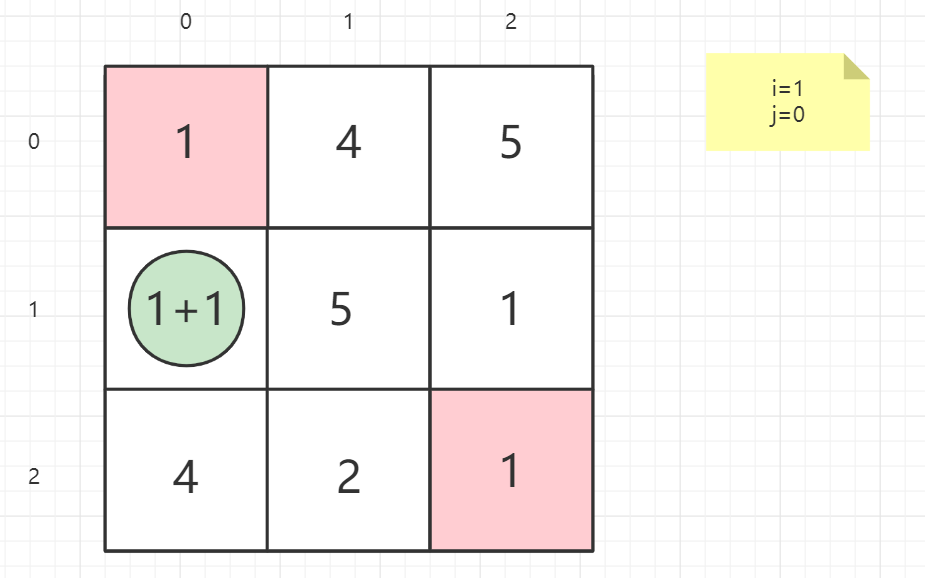
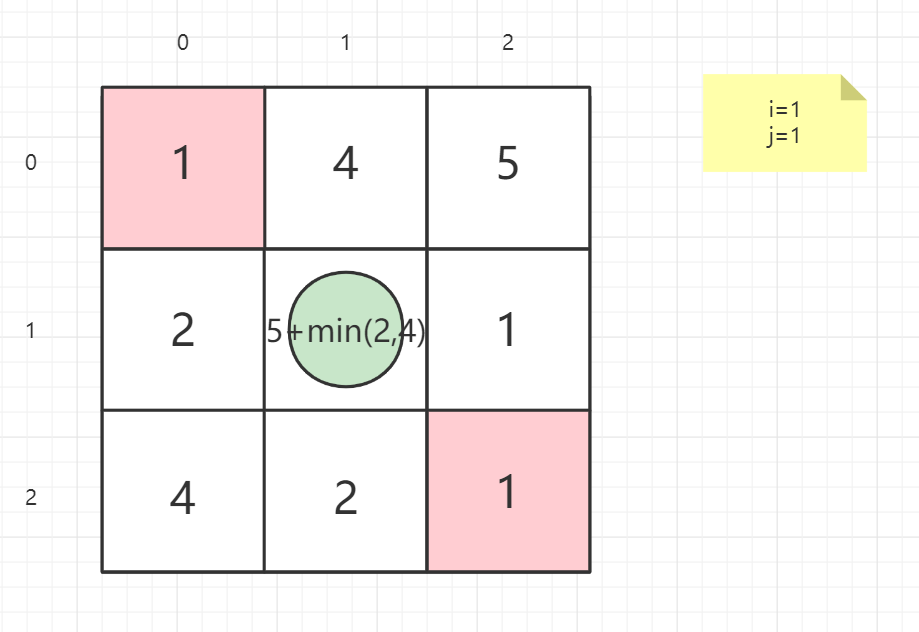
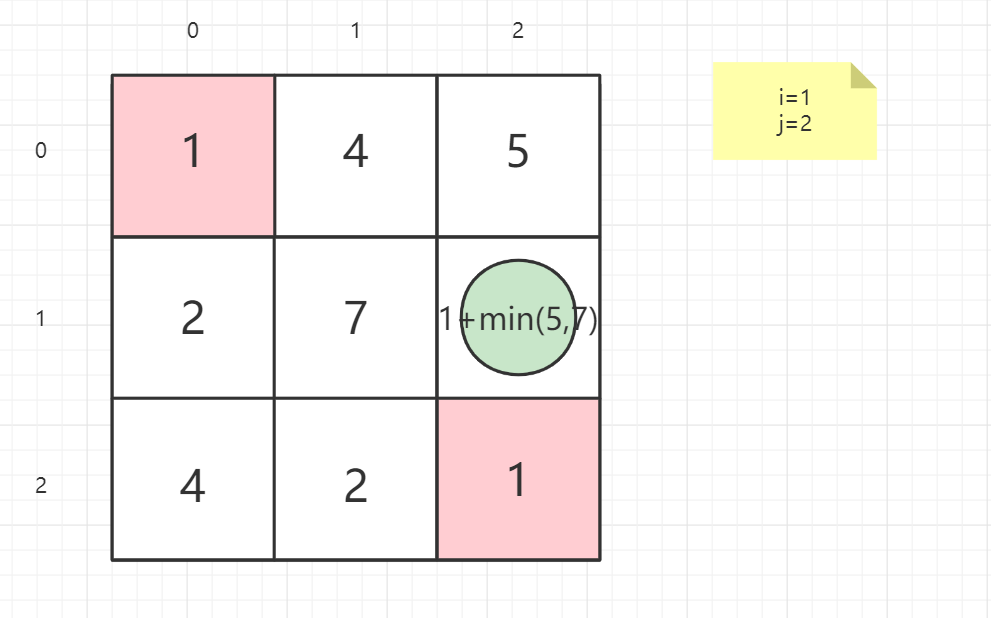
就以案例一的矩阵为例子：

1
2
3
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

逆向思维

从终点考虑问题，思考上一点在哪

最后一列是只能向上回

最后一行是只能向左回

终点不做处理

上代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int minPathSum(int[][] grid) {
        int height = grid.length;
        int width = grid[0].length;
        // 从终点往起点走
        for (int i = height - 1; i >= 0; i--) {
            for (int j = width - 1; j >= 0; j--) {
                if (i == height - 1 && j != width - 1) {
                    grid[i][j] += grid[i][j + 1];
                } else if (i != height - 1 && j == width - 1) {
                    grid[i][j] += grid[i + 1][j];
                } else if (i != height - 1 && j != width - 1) {
                    grid[i][j] += Math.min(grid[i + 1][j], grid[i][j + 1]);
                }
            }
        }
        return grid[0][0];
    }
}

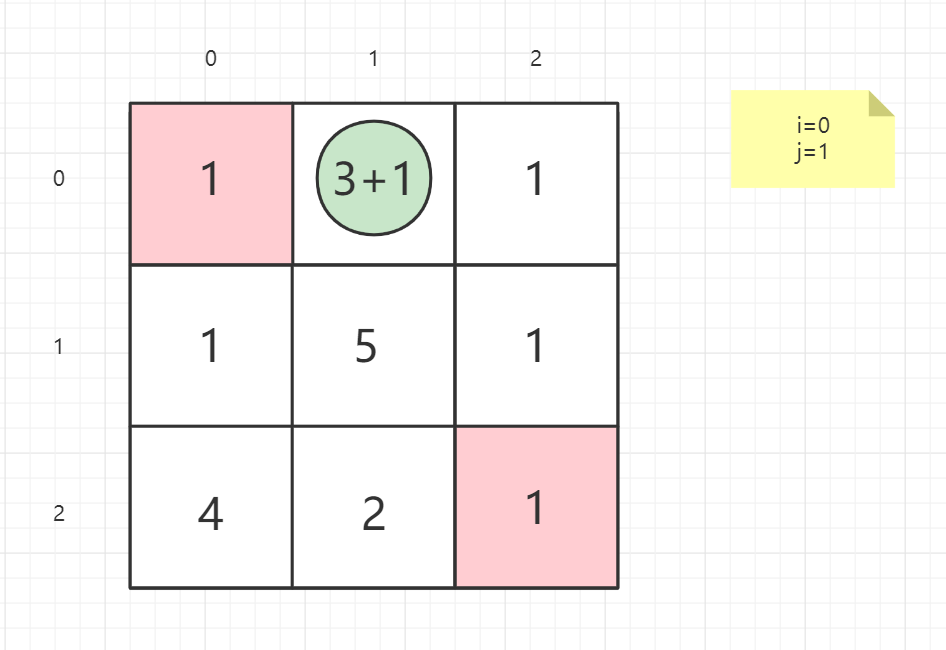
正向思维

即从起点出发，思考下一点在哪

只有第一行是可以向右

只有第一列是可以向下

起点不做处理

上代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class Solution {
    public int minPathSum(int[][] grid) {
        int rows = grid.length;
        int columns = grid[0].length;
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < columns; j++) {
                if (i == 0 && j != 0) {
                    grid[i][j] += grid[i][j - 1];
                } else if (j == 0 && i != 0) {
                    grid[i][j] += grid[i - 1][j];
                } else if (i != 0) {
                    grid[i][j] += Math.min(grid[i - 1][j], grid[i][j - 1]);
                }
            }
        }
        return grid[rows - 1][columns - 1];
    }
}

优化（状态压缩）

这是官方的优化说明：

1
2
3
4
5
我们可以用一个一维数组dp来代替二维数组，dp 数组的大小和grid的列大小相同。

这是因为对于某个固定状态，只需要考虑下方和右方的节点。

我们就可以一行一行计算，来节省空间复杂度。

这是我个人的解读（对于逆向思维）

1
2
3
想要得到最后的结果，就需要从第一行开始计算，然后该行的数据为下一行的计算提供数据。
这一行计算完成后，上一行就失去了作用，而且我们需要的就只是计算完成后的最后一行数据
返回的也就是这最后一行的最后一个数据也就是dp[rows-1][colums-1]

这里就不画流程图了，直接上代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int minPathSum(int[][] grid) {
        int rows = grid.length;
        int columns = grid[0].length;
        int[] dp = new int[columns];
        Arrays.fill(dp, Integer.MAX_VALUE);
        dp[0] = 0;
        for (int i = 0; i < rows; i++) {
            dp[0] = dp[0] + grid[i][0];
            for (int j = 1; j < columns; j++) {
                dp[j] = Math.min(dp[j], dp[j - 1]) + grid[i][j];
            }
        }
        return dp[columns - 1];
    }
}
给作者买杯咖啡吧~~~